8 Regresión discontinua
8.1 El problema de controlar por variables no observables
En la mayoría de los capítulos anteriores, vimos formas de controlar por confusores observables. Cuando hablamos de DAGs y agregar variables como covariables a un modelo de regresión o cuando usamos algún estimador de subclasificación o matching, lo que estamos haciendo es aislar la variabilidad debida a confusores observados y sustraerla de nuestra relación causal. Pero, ¿Qué pasa cuando los confusores por los que queremos controlar no son observables? Una respuesta a esta pregunta la tuvimos en el capítulo de diferencias en diferencias en el que vimos que, para un problema de una forma en particular1, la solución era estimar el contrafáctico con un grupo comparable.
1 Un problema con un tratamiento que se aplica en el tiempo y para el cual tenemos una medición antes y después para un grupo al que se le aplicó el tratamiento y una medición para los mismos puntos temporales pero para un grupo comparable (para más detalles ver el Capítulo 7).
La solución que vamos a proponer en este capítulo, al igual que en diferencias en diferencias, utiliza el contexto de mi cuasiexperimento para aislar el efecto causal.
8.2 One rule to rule them all
La idea básica detrás de la regresión discontinua es que la separación entre grupo tratamiento y control está dada por una discontinuidad en alguna variable2. Es decir, a partir de un cierto valor de esta variable un sujeto es asignado a un determinado grupo. Por ejemplo, a partir un valor de ingreso mensual, un individuo podría tener acceso a un programa de ayuda social. Supongamos que ese límite es $\(350000\) mensuales. ¿En qué se diferencian dos individuos que cobran $\(349999\) y $\(350001\) respectivamente? Probablemente en mucho, ¿no? Pero ¿y si comparamos \(100\) individuos de cada ingreso? Es bastante razonable pensar que en todas las demás características, estos individuos son comparables. Es decir, que la única diferencia entre ellos es que uno de ellos accede a un programa social y el otro no. Bueno, es en esta idea en la que se cimenta (ah bueno, se puso fino el autor) la regresión discontinua. En líneas generales vamos a comprar unidades experimentales cerquita de un lado del umbral de la running variable con unidades experimentales cerquita del otro lado del umbral.
2 Que a partir de ahora llamaremos running variable.
Empecemos a jugar con un ejemplo con datos simulados. En este ejemplo tenemos datos de la asignación de estudiantes de un curso de estadística a un programa de tutorías. La cosa es así: Los estudiantes se someten a un examen inicial y dependiendo de su puntaje, son asignados a un programa de tutorías o no. El umbral para la asignación es un puntaje de \(70\) puntos. Si el estudiante saca menos de \(70\) puntos, participa del programa de tutorías. Si saca \(70\) o más, no participa. Luego, a cada estudiante se le evalúa con un examen final. La pregunta que nos hacemos es: ¿El programa de tutorías mejora el puntaje en el examen final? Veamos qué pinta tienen los datos viendo las primeras 5 filas del dataset.
Ver el código
tutoring <- read_csv(here("data/tutoring_program.csv")) %>%
mutate(tutoring = factor(tutoring, levels = c(FALSE, TRUE),
labels = c("No", "Sí")))
#> Rows: 1000 Columns: 4
#> ── Column specification ─────────────────────────────────────────────────────
#> Delimiter: ","
#> dbl (3): id, entrance_exam, exit_exam
#> lgl (1): tutoring
#>
#> ℹ Use `spec()` to retrieve the full column specification for this data.
#> ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
tutoring %>%
head() %>%
gt()| id | entrance_exam | exit_exam | tutoring |
|---|---|---|---|
| 1 | 92.4 | 78.1 | No |
| 2 | 72.8 | 58.2 | No |
| 3 | 53.7 | 62.0 | Sí |
| 4 | 98.3 | 67.5 | No |
| 5 | 69.7 | 54.1 | Sí |
| 6 | 68.1 | 60.1 | Sí |
Por ejemplo, vemos que el estudiante de la primera fila tiene un puntaje de \(92.4\) puntos en el examen de entrada y, efectivamente, no participa en el programa de tutorías. Por otro lado, el estudiante de la tercera fila, con sus magros \(53.7\) puntos en el examen de entrada, sí participó del programa de tutorías.
Veamos las notas de entrada y como afecta eso a la participación en las tutorías:
Ver el código
rect_claro <- tibble(xmin = 65, xmax = 75, ymin = 0, ymax = 3)
ggplot(tutoring) +
# Los rectángulos
geom_rect(data = rect_claro, aes(xmin = xmin, xmax = xmax, ymin = ymin, ymax = ymax),
fill = "gray20", color = "white", alpha = .2) +
# Hacemos los puntos semitransparentes y los movemos un poco
geom_point( aes(x = entrance_exam,
y = tutoring,
color = tutoring),
size = 1.5, alpha = 0.5,
position = position_jitter(width = 0, height = 0.25, seed = 1234)) +
# Ponemos una línea vertical en el umbral
geom_vline(xintercept = 70, color = "yellow", linetype = "dashed") +
# Labels
labs(x = "Puntaje en el examen de entrada", y = "Participación en el programa de tutorías") +
# Sacó la leyenda de color
guides(color = FALSE) +
# Colores más chetos
scale_color_brewer(palette = "Dark2") +
# Theme sin fondo gris
theme_minimal()
#> Warning: The `<scale>` argument of `guides()` cannot be `FALSE`. Use "none" instead
#> as of ggplot2 3.3.4.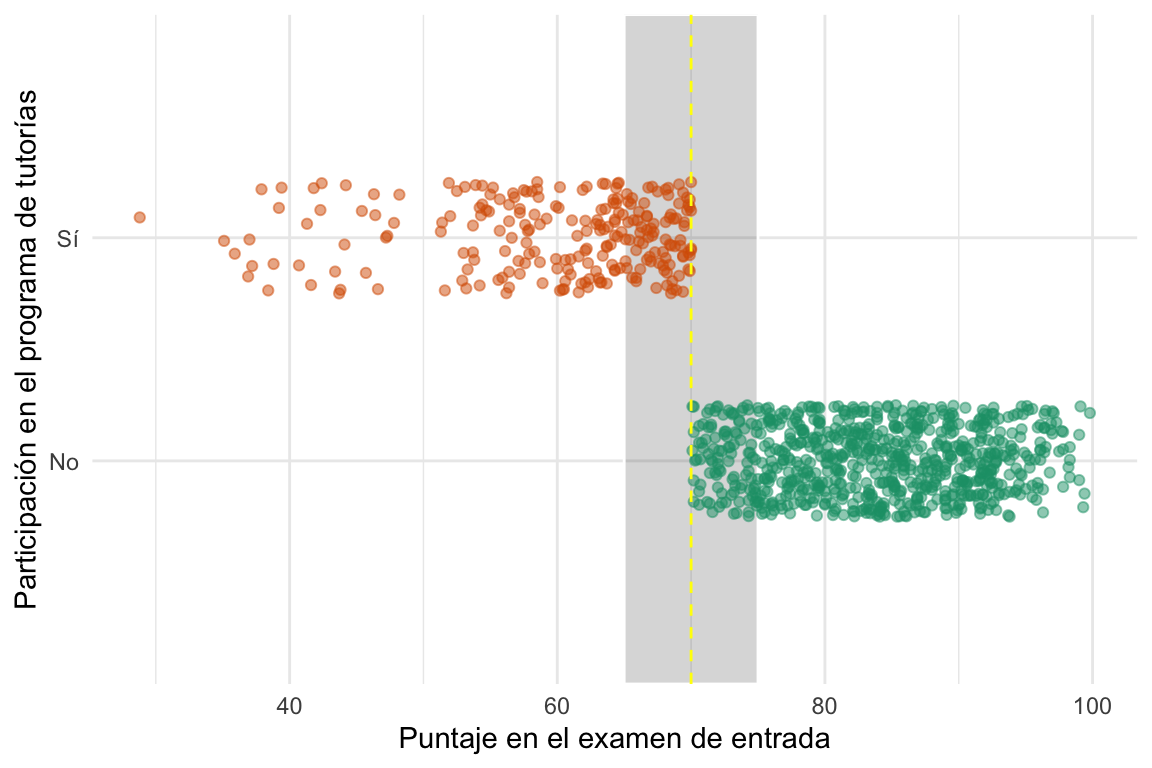
Vemos claramente que los estudiantes con más de \(70\) puntos en el examen de entrada no participan del programa de tutorías, mientras que los que sacaron menos de \(70\) sí. Parece que el umbral divide bastante bien a los grupos. Pero, pensando de nuevo en el ejemplo del ingreso, ¿qué pasa con los estudiantes que sacaron puntajes cercanos a \(70\)? ¿Son comparables? ¿Podemos asumir que la única diferencia entre ellos es la participación en el programa de tutorías? Es razonable asumir que sí.
Recordemos que la pregunta era ¿cómo afecta el programa de tutorías a la nota del examen final de los alumnos? Vamos a ver las notas de entrada y de salida de cada individuo en un gráfico. En el mismo gráfico vamos a colorear los puntos según si el estudiante participó o no del programa de tutorías y vamos a marcar como una línea vertical el umbral de \(70\) puntos en el examen de entrada.
Ver el código
# Ahora miremos como se comporta la variable outcomes en función de la running variable ####
ggplot(tutoring, aes(x = entrance_exam,
y = exit_exam,
color = tutoring,
fill = tutoring)) +
geom_point(size = 1.5, alpha = .3) +
# Ponemos una línea vertical en el umbral
geom_vline(xintercept = 70, color = "steelblue", linetype = "dashed") +
# Las lables
labs(x = "Puntaje en el examen de entrada",
y = "Puntaje en el examen de salida",
color = "Participó en la tutoría",
fill = "Participó en la tutoría") +
# Colores más chetos
scale_color_brewer(palette = "Dark2") +
scale_fill_brewer(palette = "Dark2") +
# Theme sin fondo gris
theme_minimal() +
theme(legend.position = "top")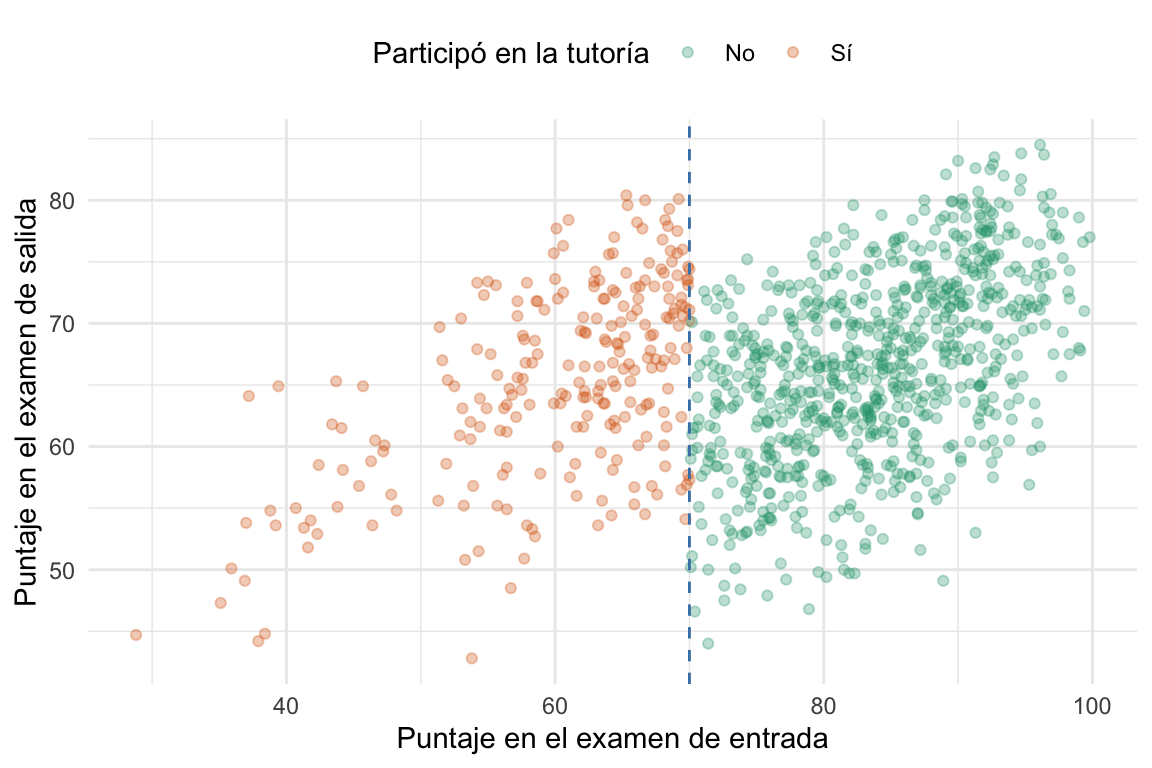
Pareciera que hay una relación entre la nota de entrada y de salida. Esto tiene bastante sentido, ya que es esperable que los estudiantes a los que les fue bien a la entrada les vaya bien a la salida. Pero también se ve otra cosa, en esta relación entre ambas notas puede verse una discontinuidad en el umbral de \(70\) puntos. Es decir, parece que los estudiantes que participaron del programa de tutorías tienen un puntaje más alto en el examen de salida, para mismo puntaje en el examen de entrada, que los que no participaron. Tracemos unas líneas y veamos si esto es así.
Ver el código
# Ahora miremos como se comporta la variable outcomes en función de la running variable ####
ggplot(tutoring, aes(x = entrance_exam,
y = exit_exam,
color = tutoring,
fill = tutoring)) +
geom_point(size = 1.5, alpha = .3) +
# Agregamos una linea basada en un modelo lineal para la running variable menor a 70
geom_smooth(data = filter(tutoring, entrance_exam <= 70), method = "lm") +
# Agregamos una linea basada en un modelo lineal para la running variable mayor a 70
geom_smooth(data = filter(tutoring, entrance_exam > 70), method = "lm") +
# Ponemos una línea vertical en el umbral
geom_vline(xintercept = 70, color = "steelblue", linetype = "dashed") +
# Las lables
labs(x = "Puntaje en el examen de entrada",
y = "Puntaje en el examen de salida",
color = "Participó en la tutoría",
fill = "Participó en la tutoría") +
# Colores más chetos
scale_color_brewer(palette = "Dark2") +
scale_fill_brewer(palette = "Dark2") +
# Theme sin fondo gris
theme_minimal() +
theme(legend.position = "top")
#> `geom_smooth()` using formula = 'y ~ x'
#> `geom_smooth()` using formula = 'y ~ x'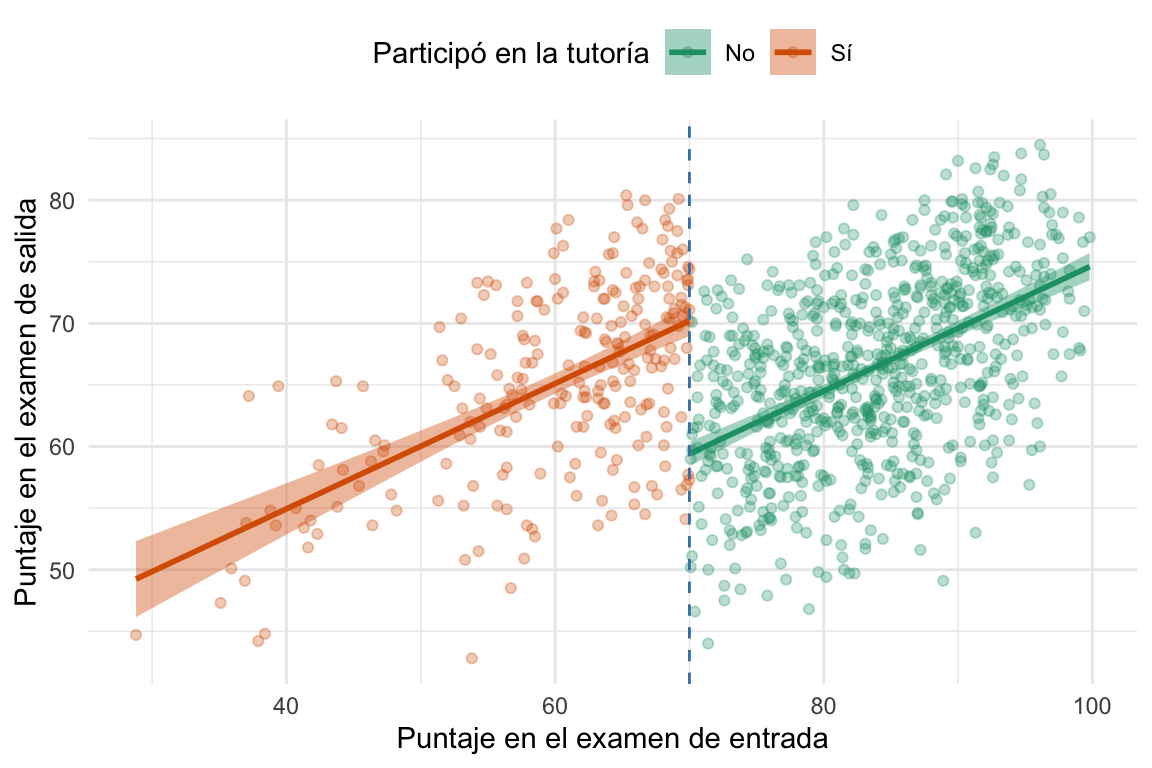
Vemos que efectivamente, la línea de regresión para los estudiantes que participaron del programa de tutorías es más alta que la de los que no participaron, mostrando que hubo un efecto del programa de tutorías en la relación entre la nota de entrada y de salida. Pero, ¿cómo podemos estimar este efecto? ¿No dijimos que los estudiantes que eran comparables eran los que estaban cerca del umbral? Dejemos esta última pregunta para más adelante y avancemos con la estimación del efecto del programa de tutorías.
En la siguiente figura vemos que la diferencia en el umbral, luego de ajustar una recta a cada grupo de estudiantes, es la que nos da el efecto del programa de tutorías. En este caso no deja de ser la diferencia de ordenadas al origen de las rectas ajustadas a cada grupo, pero ya vamos a ver que no siempre es así.
Ver el código
tutoring_centered <- tutoring |>
mutate(entrance_centered = entrance_exam - 70)
modelo_lm <- lm(exit_exam ~ entrance_centered + tutoring,
data = tutoring_centered)
ggplot(tutoring, aes(x = entrance_exam,
y = exit_exam,
color = tutoring,
fill = tutoring)) +
geom_point(size = 1.5, alpha = .3) +
# Agregamos una linea basada en un modelo lineal para la running variable menor a 70
geom_smooth(data = filter(tutoring, entrance_exam <= 70), method = "lm") +
# Agregamos una linea basada en un modelo lineal para la running variable mayor a 70
geom_smooth(data = filter(tutoring, entrance_exam > 70), method = "lm") +
# Ponemos una línea vertical en el umbral
geom_vline(xintercept = 70, color = "steelblue", linetype = "dashed") +
# Un segmento con el efecto del modelo
geom_segment(aes(x = 70, y = modelo_lm$coefficients[1],
xend = 70, yend = modelo_lm$coefficients[1] + modelo_lm$coefficients[3]),
color = "darkblue", linewidth = 2) +
annotate("label",
x = 75, y = modelo_lm$coefficients[1] + modelo_lm$coefficients[3]/2,
label = "LATE",
color = "darkblue", size = 4, hjust = 0.5) +
# Las lables
labs(x = "Puntaje en el examen de entrada",
y = "Puntaje en el examen de salida",
color = "Participó en la tutoría",
fill = "Participó en la tutoría") +
# Colores más chetos
scale_color_brewer(palette = "Dark2") +
scale_fill_brewer(palette = "Dark2") +
# Theme sin fondo gris
theme_minimal() +
theme(legend.position = "top")
#> `geom_smooth()` using formula = 'y ~ x'
#> `geom_smooth()` using formula = 'y ~ x'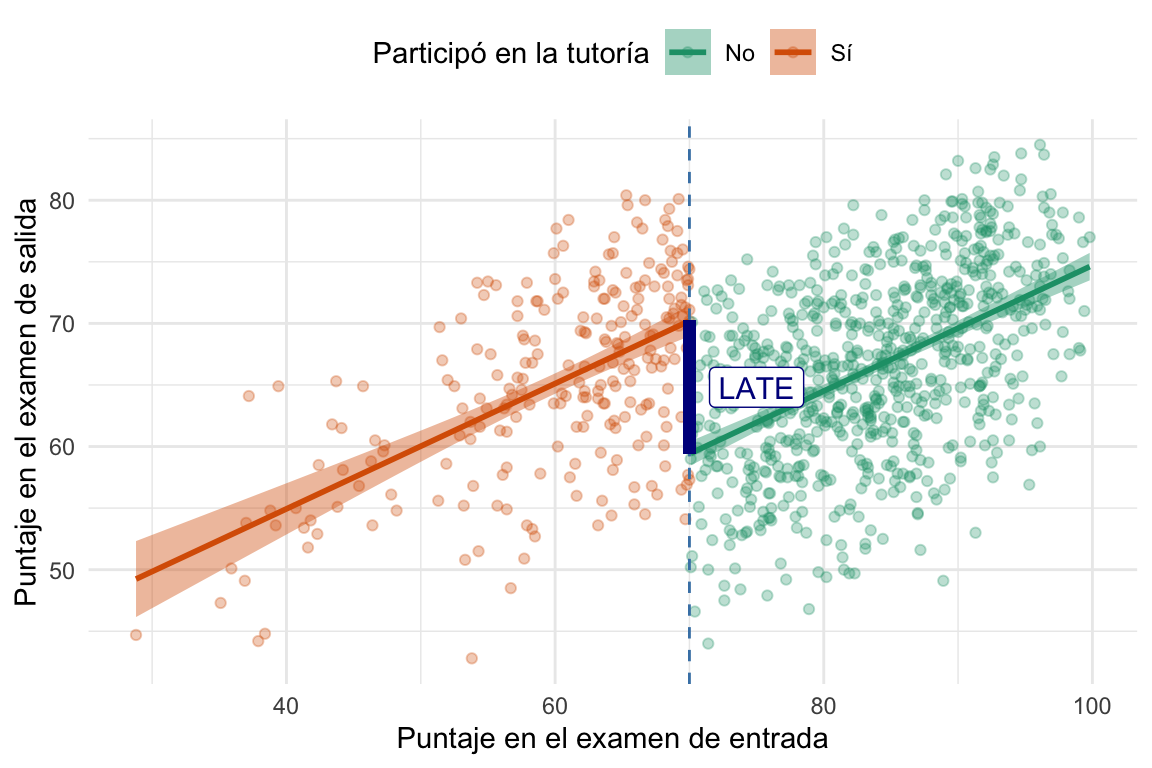
En la figura llamamos al efecto LATE3, pero, ¿qué tiene de local el efecto? Bueno, como vamos a desarrollar un poco más adelante, ese efecto es local porque, en teoría, sólo tiene validez para los individuos que están a un lado u otro del umbral. Es decir, no representa el efecto a individuos que están lejos del umbral. Sin embargo, y como en todas estas cosas, podemos justificar que ese efecto sí es válido para individuos que están un poco más lejos del umbral, pero eso requiere que conozcamos el problema.
3 Del inglés Local Average Treatment Effect.
Creo que, si bien se deben estar creyendo lo que les cuento, también deben tener un millón y medio de preguntas sobre cómo se calcula este hermoso LATE y qué condiciones debe cumplir la running variable y el sesgo. Para eso nos queda una buena parte del capítulo, pero por ahora me quedo contento con que la idea detrás del método es: Las unidades experimentales a uno y otro lado del umbral son, en promedio, comparables en todas las características observadas y no observadas salvo en la asignación o no al tratamiento.
8.3 Un ejemplo con los husos4 horarios4 Sí, es husos y no usos, no es un typo.
4 Sí, es husos y no usos, no es un typo.
Exiten múltiples ejemplos en la literatura científica del uso de regresión discontinua para estimar el efecto causal de un tratamiento en datos observacionales. Políticas públicas, programas sociales, programas educativos, etc. Pero en esta sección les voy a contar un ejemplo que utiliza una running variable un tanto particular: los husos horarios.
Este trabajo (Schafer y Holbein (2020)) analiza cómo las restricciones de tiempo (horarios escolares, laborales, etc.) afectan la participación electoral en los Estados Unidos (un tema muy relevante ya que el voto no es obligatorio), utilizando un diseño de regresión discontinua geográfica que aprovecha las fronteras de las zonas horarias de EE. UU. como discontinuidades. En este diseño, el umbral es la línea divisoria de la zona horaria. La running variable es la distancia geográfica bidimensional, específicamente la distancia latitudinal y longitudinal (medida en grados) desde el centro de un condado hasta la frontera de la zona horaria más cercana.
Veamos como muestran esto gráficamente en el artículo:
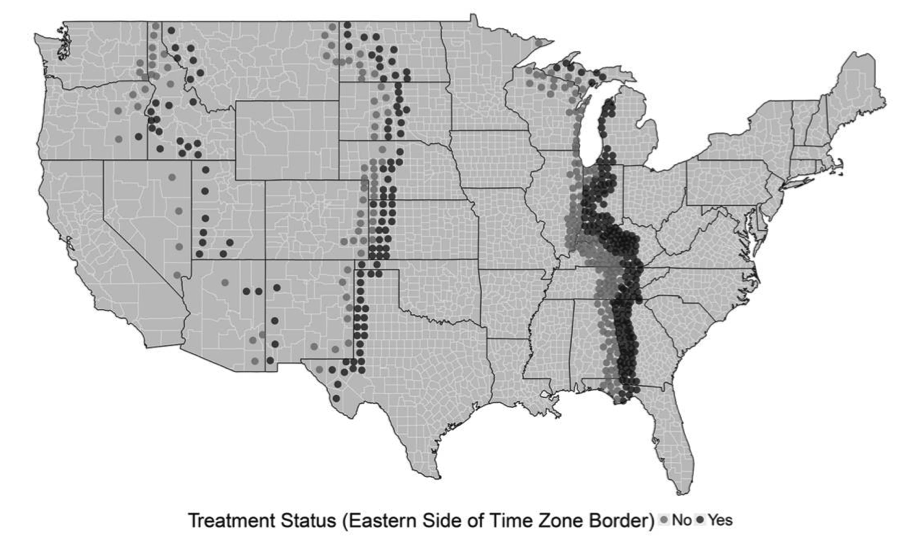
Esto significa que a un lado y al otro de la zona horaria los condados son comparables en todas las características observadas y no observadas, salvo en la zona horaria y el efecto de ella en las restricciones de tiempo. Es decir, que los condados a un lado y al otro de la frontera horaria son comparables en todas las características excepto en la hora local.
Aprovechando esto, los autores estiman el efecto con un modelo de regresión discontinua5. En la figura siguiente se puede ver cómo se comporta la participación electoral en función de la distancia a la frontera horaria:
5 Para detalles del ajuste pueden ver el código que acompaña a la Figura 8.2.
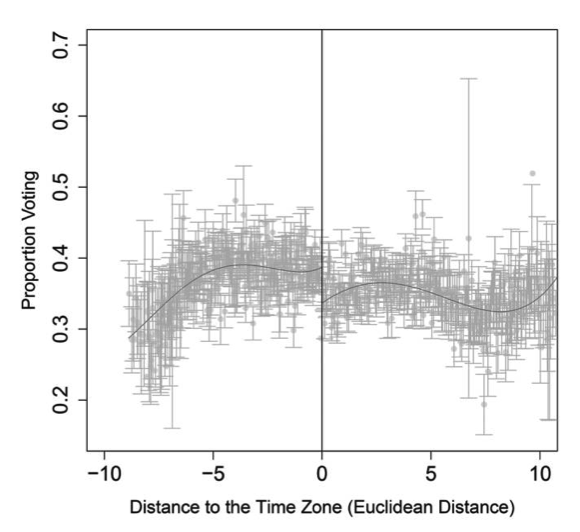
Es con estas herramientas que el estudio concluye que los ciudadanos que viven en el lado inmediatamente oriental de una frontera horaria votan significativamente menos (entre \(1.5\) y \(3\) puntos porcentuales) que aquellos en el lado occidental.
8.4 ¿Cómo se estima el efecto causal?
Si vemos la Figura 8.1, podemos ver que la diferencia entre las dos rectas es el efecto del programa de tutorías. Pero, ¿cómo se estima? Bueno, la forma más sencilla de hacerlo es ajustar un modelo lineal a los datos y calcular la diferencia entre las ordenadas al origen de las rectas ajustadas a cada grupo. Pero esta no es la única forma de calcular el LATE. En lo que sigue vamos a explorar variantes de esta estimación y ver cómo afectan en el efecto estimado.
8.4.1 Estimación paramétrica
Una de las alternativas que tenemos es hacer una estimación paramétrica o no paramétrica. Pero, ¿a qué nos referimos con esto? En una estimación paramétrica, como la que vimos en el ejemplo anterior, ajustamos un modelo a los datos que está definido por parámetros, como podría ser un modelo lineal.
El primer modelo que vamos a ajustar es el siguiente:
\[ y = \beta_0 + \beta_1 \text{Running variable (centrada)} + \beta_2 \text{indicadora del tratamiento} \]
Que en nuestro caso sería más bien:
\[ nota_{salida} = \beta_0 + \beta_1 (nota_{entrada}-70) + \beta_2 \mathbb{I}_{tutoria} \]
donde \(\mathbb{I}_{tutoria}\) es una variable indicadora que toma el valor de \(1\) si el estudiante participó del programa de tutorías y \(0\) si no, \(nota_{entrada}\) es la nota del examen de entrada y \(nota_{salida}\) es la nota del examen de salida. Pero ¿por qué le restamos \(70\) a la nota de entrada? Bueno, porque queremos centrar la running variable en el umbral. Es decir, queremos que el umbral sea \(0\) y que los valores a la izquierda del umbral sean negativos y los valores a la derecha sean positivos. Esto nos va a permitir interpretar mejor los coeficientes del modelo6.
6 En realidad, no es necesario centrar la running variable cuando el ajuste es una recta, pero cuando no lo es, queremos que la diferencia en ordenadas al origen (cuando la running variable vale \(0\)) sea el LATE. Igualmente es una buena práctica centrar la running variable.
Ver el código
modelsummary(list("Lineal"= modelo_lm),
coef_rename = c("entrance_centered" = "Nota inicial centrada",
"tutoringSí" = "Participó en la tutoría"),
statistic = NULL,
gof_omit = ".*",
output = "gt") |>
gt_highlight_rows(rows = 3,
fill = "lightyellow",
font_weight = "bold")| Lineal | |
|---|---|
| (Intercept) | 59.411 |
| Nota inicial centrada | 0.510 |
| Participó en la tutoría | 10.800 |
Estimaciones del LATE utilizando un modelo lineal.
El coeficiente de la variable indicadora del tratamiento es el LATE. En este caso, el modelo nos dice que el programa de tutorías aumenta en 10.8 puntos la nota del examen de salida, en promedio, para los estudiantes que están cerca del umbral. Si vemos la Figura 8.1, podemos ver que esta estimación tiene sentido.
También podríamos ajustar otro modelo lineal7, en el que suponemos que la relación entre la running variable y el resultado es cuadrática. No vamos a escribir el modelo porque se complica un poco ya que ajustamos una parábola a cada lado de la discontinuidad. Pero la idea es la misma: ajustamos un modelo lineal a los datos y calculamos la diferencia entre las estimaciones de los modelos para el umbral (la running variable centrada igual a 0)8.
7 ¿Por qué esto sigue siendo un modelo lineal?
8 Para detalles del ajuste pueden ver el código que acompaña a la Figura 8.2.
Ver el código
tutoring_centered <- tutoring_centered |>
mutate(entrance_centered_2 = entrance_centered^2,
entrance_centered_3 = entrance_centered^3)
modelo_sq_1 <- lm(exit_exam ~ entrance_centered_2,
data = tutoring_centered %>%
filter(entrance_centered <= 0))
modelo_sq_2 <- lm(exit_exam ~ entrance_centered_2,
data = tutoring_centered %>%
filter(entrance_centered > 0))
modelo_cub_1 <- lm(exit_exam ~ entrance_centered_3,
data = tutoring_centered %>%
filter(entrance_centered <= 0))
modelo_cub_2 <- lm(exit_exam ~ entrance_centered_3,
data = tutoring_centered %>%
filter(entrance_centered > 0))
tutoring_centered <- tutoring_centered %>%
add_predictions(modelo_lm, var = "exit_pred_lm") %>%
add_predictions(modelo_sq_1, var = "exit_pred_sq1") %>%
add_predictions(modelo_sq_2, var = "exit_pred_sq2") %>%
add_predictions(modelo_cub_1, var = "exit_pred_cub1") %>%
add_predictions(modelo_cub_2, var = "exit_pred_cub2")
colors <- c("Lineal" = "darkgreen",
"Cuadrático" = "darkred",
"Cúbico" = "darkorange")
ggplot(tutoring_centered, aes(x = entrance_centered,
y = exit_exam)) +
geom_point(size = 1.5, alpha = .2) +
# Agregamos una linea basada en un modelo lineal para la running variable centrada menor a 0
geom_line(aes(y = exit_pred_lm, color = "Lineal"), linewidth = 1) +
# Agregamos una linea basada en un modelo lineal para la running variable centrada al cuadrado menor a 0
geom_line(data = filter(tutoring_centered, entrance_centered <= 0), aes(y = exit_pred_sq1, color = "Cuadrático"),
linewidth = 1) +
# Agregamos una linea basada en un modelo lineal para la running variable centrada al cuadrado mayor a 0
geom_line(data = filter(tutoring_centered, entrance_centered > 0), aes(y = exit_pred_sq2, color = "Cuadrático"),
linewidth = 1) +
# Agregamos una linea basada en un modelo lineal para la running variable centrada al cubo menor a 0
geom_line(data = filter(tutoring_centered, entrance_centered <= 0), aes(y = exit_pred_cub1, color = "Cúbico"),
linewidth = 1) +
# Agregamos una linea basada en un modelo lineal para la running variable centrada al cubo mayor a 0
geom_line(data = filter(tutoring_centered, entrance_centered > 0), aes(y = exit_pred_cub2, color = "Cúbico"),
linewidth = 1) +
# Ponemos una línea vertical en el umbral
geom_vline(xintercept = 0, color = "steelblue", linetype = "dashed") +
# Las lables
labs(x = "Puntaje en el examen de entrada (centrado)",
y = "Puntaje en el examen de salida",
color = NULL,
fill = "Participó en la tutoría") +
# Colores más chetos
scale_color_manual(values = colors) +
#scale_color_brewer(palette = "Dark2") +
scale_fill_brewer(palette = "Dark2") +
# Theme sin fondo gris
theme_minimal() +
theme(legend.position = "top")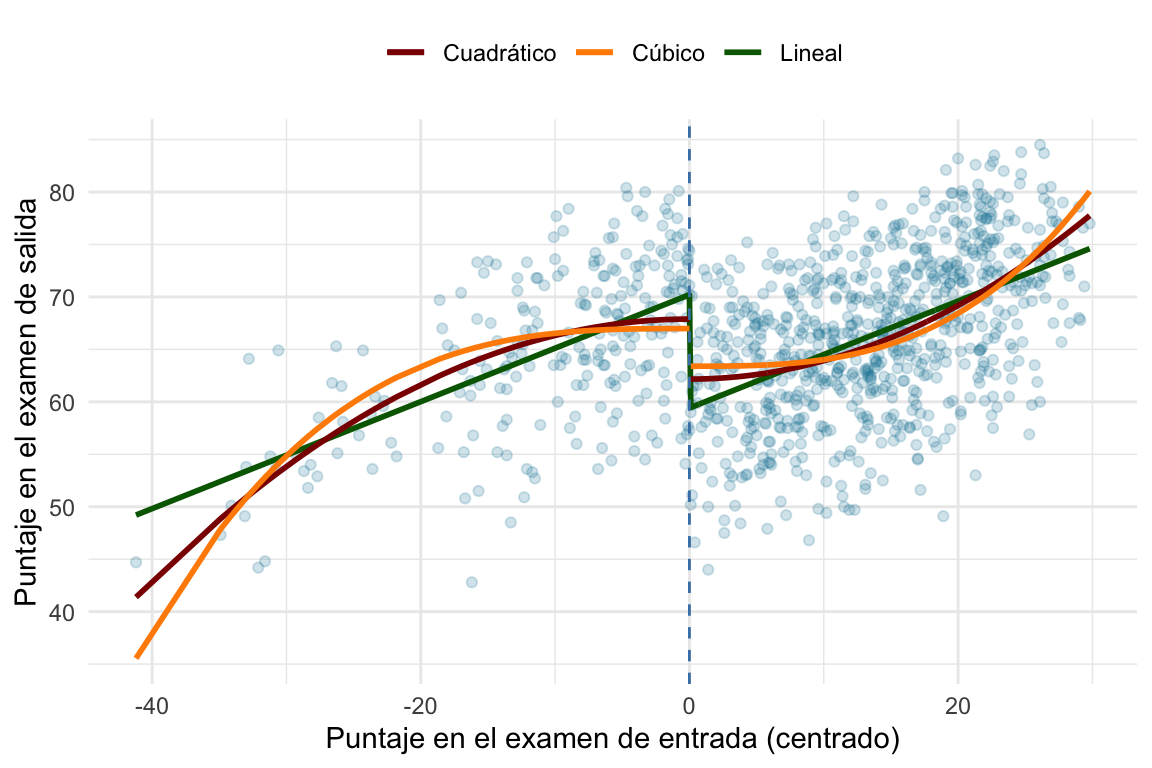
Como vemos en la Figura 8.2, depende cómo ajustemos el modelo, el efecto del programa de tutorías cambia. En este caso, el ajuste lineal nos da un efecto de 3.6, el cuadrático de 5.7 y el cúbico de 3.6. Es decir, la elección de cómo ajustamos a los datos a cada lado del umbral afecta mi LATE.
Entonces: ¿Cómo decidimos qué ajuste usar? Esto, como vamos a ver más adelante no tiene una respuesta concreta, hay que ver los datos y, más importante aún, ver cuán sensibles son nuestros resultados a estas elecciones. Por ejemplo, si al pasar de una recta a una parábola el efecto pasa de \(100\) a \(0\), entonces es probable que la elección de la forma de ajuste sea importante y debamos justificarla. Si, por el contrario, el efecto no cambia mucho, entonces podemos estar más tranquilos.
Ver el código
# Armo una tabla con los valores de los ajustes
tutoring_centered %>%
summarise("Lineal" = round(predict(modelo_lm, newdata = tibble(entrance_centered = 0, tutoring = "Sí")) - predict(modelo_lm, newdata = tibble(entrance_centered = 0, tutoring = "No")), 1),
"Cuadrático" = round(predict(modelo_sq_1, newdata = tibble(entrance_centered_2 = 0)) -
predict(modelo_sq_2, newdata = tibble(entrance_centered_2 = 0)), 1),
"Cúbico" = round(predict(modelo_cub_1, newdata = tibble(entrance_centered_3 = 0)) -
predict(modelo_cub_2, newdata = tibble(entrance_centered_3 = 0)), 1)) %>%
pivot_longer(everything(), names_to = "Modelo", values_to = "LATE") %>%
gt() |>
tab_header(title = "Estimaciones del LATE para distintos ajustes") %>%
fmt_number(columns = vars(LATE), decimals = 1) %>%
gt_highlight_cols(columns = 2,
fill = "lightyellow",
font_weight = "bold")
#> Warning: Since gt v0.3.0, `columns = vars(...)` has been deprecated.
#> • Please use `columns = c(...)` instead.| Estimaciones del LATE para distintos ajustes | |
| Modelo | LATE |
|---|---|
| Lineal | 10.8 |
| Cuadrático | 5.7 |
| Cúbico | 3.6 |
Tabla con las estimaciones de los distintos ajustes.
8.4.2 Ancho de banda
Volvamos a la idea de por qué usamos todos los datos si en realidad queremos comparar a un lado y otro del umbral. Bueno, una forma de lidiar con esto es limitar el análisis a un cierto rango de la running variable. Es decir, podemos decidir que sólo vamos a comparar a los estudiantes que están dentro de un cierto rango del umbral. Por ejemplo, podríamos decidir que sólo vamos a comparar a los estudiantes que están entre \(65\) y \(75\) puntos en el examen de entrada. Esto se conoce como ancho de banda y es una forma de limitar el análisis a los estudiantes que están más cerca del umbral.
Repitamos el ajuste lineal de los estudiantes de cada lado del umbral pero limitando el ancho de banda. Primero con ancho de banda total, luego con ancho de banda de \(10\) punto (es decir, sólo analizando los datos entre \(60\) y \(80\) puntos) y finalmente con un ancho de banda de \(5\) puntos (es decir, sólo analizando los datos entre \(65\) y \(75\) puntos).
Ver el código
# Ahora probemos bajando el bandwidth
# BW = 10
model_bw_10 <- lm(exit_exam ~ entrance_centered + tutoring,
data = filter(tutoring_centered,
entrance_centered >= -10 &
entrance_centered <= 10))
tidy(model_bw_10)
#> # A tibble: 3 × 5
#> term estimate std.error statistic p.value
#> <chr> <dbl> <dbl> <dbl> <dbl>
#> 1 (Intercept) 60.4 0.752 80.3 2.99e-249
#> 2 entrance_centered 0.388 0.114 3.40 7.45e- 4
#> 3 tutoringSí 9.27 1.31 7.09 6.27e- 12
# BW = 5
model_bw_5 <- lm(exit_exam ~ entrance_centered + tutoring,
data = filter(tutoring_centered,
entrance_centered >= -5 &
entrance_centered <= 5))
tidy(model_bw_5)
#> # A tibble: 3 × 5
#> term estimate std.error statistic p.value
#> <chr> <dbl> <dbl> <dbl> <dbl>
#> 1 (Intercept) 60.6 1.12 54.3 4.78e-118
#> 2 entrance_centered 0.380 0.331 1.15 2.53e- 1
#> 3 tutoringSí 9.12 1.91 4.77 3.66e- 6
# Veamos el ajuste de cada uno de estos modelos
# Full BW
p_full <- ggplot(tutoring, aes(x = entrance_exam,
y = exit_exam,
color = tutoring,
fill = tutoring)) +
geom_point(size = 1.5, alpha = 0.5) +
# Add a line based on a linear model for the people scoring 70 or less
geom_segment(x = min(tutoring$entrance_exam), xend = 70,
y = modelo_lm$coefficients[1]+min(tutoring_centered$entrance_centered)*modelo_lm$coefficients[2] +
modelo_lm$coefficients[3],
yend = modelo_lm$coefficients[1] + modelo_lm$coefficients[3],
color = "gray30", linewidth = 1) +
# Add a line based on a linear model for the people scoring more than 70
geom_segment(x = 70, xend = max(tutoring$entrance_exam),
y = modelo_lm$coefficients[1],
yend = modelo_lm$coefficients[1] + modelo_lm$coefficients[2]*max(tutoring_centered$entrance_centered),
color = "gray30", linewidth = 1) +
# Ponemos una línea vertical en el umbral
geom_vline(xintercept = 70, color = "darkblue", linetype = "dashed") +
# Las labels
labs(x = NULL,
y = NULL,
color = "Participó en la tutoría",
fill = "Participó en la tutoría") +
# Colores más chetos
scale_color_brewer(palette = "Dark2") +
scale_fill_brewer(palette = "Dark2") +
# Theme sin fondo gris
theme_minimal() +
theme(legend.position = "none")
# BW = 10
p_bw10 <- tutoring_centered |>
dplyr::filter(between(entrance_centered, -10, 10)) |>
ggplot(aes(x = entrance_exam,
y = exit_exam,
color = tutoring,
fill = tutoring)) +
geom_point(size = 1.5, alpha = 0.5) +
geom_point(data = tutoring_centered |>
dplyr::filter(!between(entrance_centered, -10, 10)),
size = 1.5, alpha = 0.3, color = "gray") +
# Add a line based on a linear model for the people scoring 70 or less
geom_segment(x = 60, xend = 70,
y = model_bw_10$coefficients[1]-10*model_bw_10$coefficients[2] +
model_bw_10$coefficients[3],
yend = model_bw_10$coefficients[1] + model_bw_10$coefficients[3],
color = "gray30", linewidth = 1) +
# Add a line based on a linear model for the people scoring more than 70
geom_segment(x = 70, xend = 80,
y = model_bw_10$coefficients[1],
yend = model_bw_10$coefficients[1] + model_bw_10$coefficients[2]*10,
color = "gray30", linewidth = 1) +
# Ponemos una línea vertical en el umbral
geom_vline(xintercept = 70, color = "darkblue", linetype = "dashed") +
# Las labels
labs(x = NULL,
y = "Puntaje en el examen de salida",
color = "Participó en la tutoría",
fill = "Participó en la tutoría") +
# Colores más chetos
scale_color_brewer(palette = "Dark2") +
scale_fill_brewer(palette = "Dark2") +
# Theme sin fondo gris
theme_minimal() +
theme(legend.position = "none")
# BW = 5
p_bw5 <- tutoring_centered |>
dplyr::filter(between(entrance_centered, -5, 5)) |>
ggplot(aes(x = entrance_exam,
y = exit_exam,
color = tutoring,
fill = tutoring)) +
geom_point(size = 1.5, alpha = 0.5) +
geom_point(data = tutoring_centered |>
dplyr::filter(!between(entrance_centered, -5, 5)),
size = 1.5, alpha = 0.3, color = "gray") +
# Add a line based on a linear model for the people scoring 70 or less
geom_segment(x = 65, xend = 70,
y = model_bw_5$coefficients[1]-5*model_bw_5$coefficients[2] +
model_bw_5$coefficients[3],
yend = model_bw_5$coefficients[1] + model_bw_5$coefficients[3],
color = "gray30", linewidth = 1) +
# Add a line based on a linear model for the people scoring more than 70
geom_segment(x = 70, xend = 75,
y = model_bw_5$coefficients[1],
yend = model_bw_5$coefficients[1] + model_bw_5$coefficients[2]*5,
color = "gray30", linewidth = 1) +
# Ponemos una línea vertical en el umbral
geom_vline(xintercept = 70, color = "darkblue", linetype = "dashed") +
# Las labels
labs(x = "Puntaje en el examen de entrada",
y = NULL,
color = "Participó en la tutoría",
fill = "Participó en la tutoría") +
# Colores más chetos
scale_color_brewer(palette = "Dark2") +
scale_fill_brewer(palette = "Dark2") +
# Theme sin fondo gris
theme_minimal() +
theme(legend.position = "none")
library(patchwork)
p_full / p_bw10 / p_bw5 + plot_layout(guides = "collect")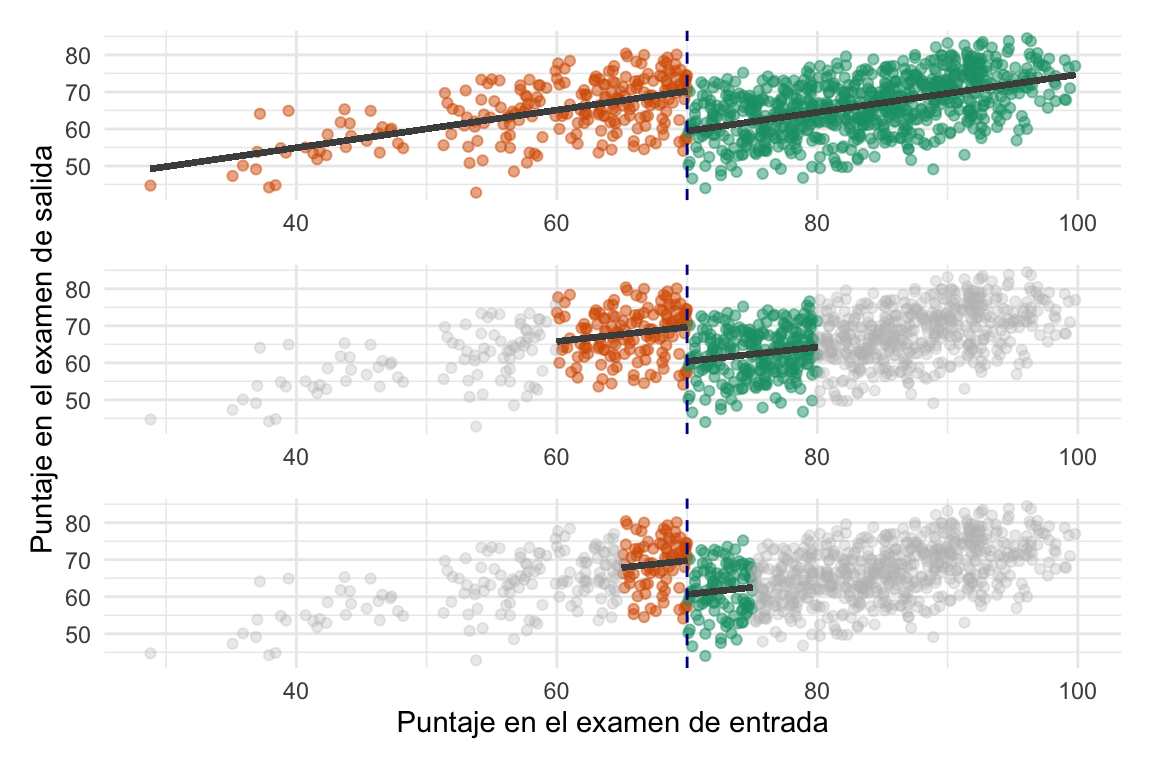
En la figura vemos que los ajustes son ligeramente distintos, pero no se llega a ver una difrencia. Qué pasa si vemos las estimaciones del modelo:
Ver el código
# Las estimaciones y el sample size
modelsummary(list("Full data" = modelo_lm,
"Bandwidth = 10" = model_bw_10,
"Bandwidth = 5" = model_bw_5),
coef_rename = c("entrance_centered" = "Nota inicial centrada",
"tutoringSí" = "Participó en la tutoría"),
gof_omit = 'DF|Deviance|R2|AIC|BIC|Log.Lik|F|RMSE',
statistic = "p = {p.value}",
output = "gt") |>
gt_highlight_rows(rows = 5,
fill = "lightyellow",
font_weight = "bold") |>
gt_highlight_rows(rows = 7,
fill = "lightyellow",
font_weight = "bold")| Full data | Bandwidth = 10 | Bandwidth = 5 | |
|---|---|---|---|
| (Intercept) | 59.411 | 60.377 | 60.631 |
| p = <0.001 | p = <0.001 | p = <0.001 | |
| Nota inicial centrada | 0.510 | 0.388 | 0.380 |
| p = <0.001 | p = <0.001 | p = 0.253 | |
| Participó en la tutoría | 10.800 | 9.273 | 9.122 |
| p = <0.001 | p = <0.001 | p = <0.001 | |
| Num.Obs. | 1000 | 404 | 194 |
Hay tres cosas que quiero que vean. Primero, que el LATE es bastante similar en los tres casos pero se ve afectado por el ancho de banda. Segundo, el ancho de banda afecta el tamaño de la muestra y, por lo tanto, la potencia estadística. Y tercero, algo de lo que no habíamos hablado hasta el momento era de la variabilidad de las estimaciones. Por ejemplo, en este caso que el LATE es un parámetro de un modelo lineal como los que ya conocemos, podemos utilizar las herramientas usuales de inferencia estadística (como el p-valor que ven abajo de la estimación en la tabla) para sacar conclusiones al respecto.
8.4.3 Kernels
Como vimos, achicar el ancho de banda mejoraría la estimación (porque estamos considerando a los sujetos más “parecido”) pero disminuye el tamaño de muestra efectivo. Una alternativa a esto es conservar el ancho de banda pero darle más peso a los puntos que están cerca del umbral. Por ejemplo, podríamos darle más peso a los puntos que están a \(1\) punto del umbral que a los que están a \(10\) puntos. Esto se hace utilizando un kernel. Un kernel es una función que asigna un peso a cada punto en función de su distancia al umbral. Los kernels pueden tener diversas formas, como triangular o gaussiano9.
9 Cuando achicamos el ancho de banda en la sección anterior podemos considerar como si hubiéramos utilizado un kernel rectangular, es decir, que todos los puntos dentro del ancho de banda tienen el mismo peso.
Dejenme mostrarles la forma de algunos kernels que vamos a probar:
Ver el código
kernels <- tibble(x = seq(-1.5, 1.5, length.out = 200)) %>%
mutate(rectangular = ifelse(abs(x) <= 1, 1, 0),
triangular = ifelse(abs(x) <= 1, 1 - abs(x), 0),
epanechnikov = ifelse(abs(x) <= 1, 0.75 * (1 - x^2), 0))
ggplot(kernels, aes(x = x)) +
geom_line(aes(y = rectangular, color = "Rectangular"), size = 1) +
geom_line(aes(y = triangular, color = "Triangular"), size = 1) +
geom_line(aes(y = epanechnikov, color = "Epanechnikov"), size = 1) +
labs(x = "Distancia al umbral", y = "Peso", color = NULL) +
scale_color_brewer(palette = "Dark2") +
theme_minimal() +
theme(legend.position = "top")
#> Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
#> ℹ Please use `linewidth` instead.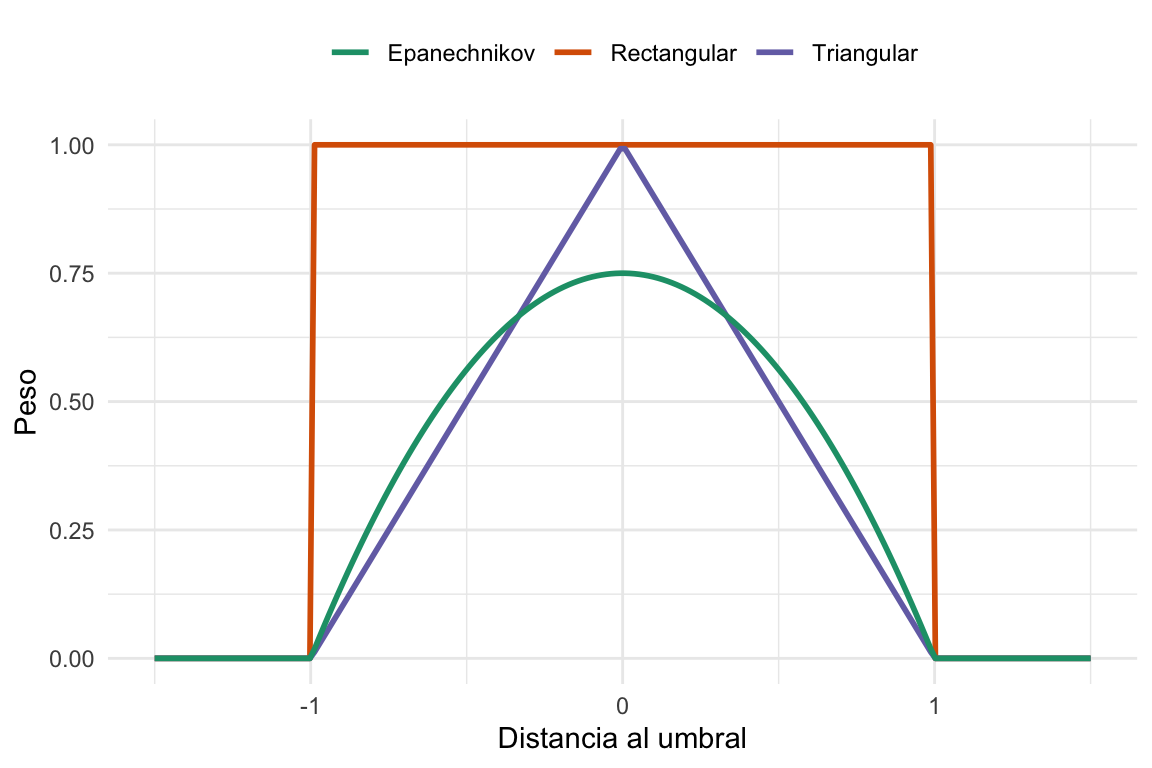
Podemos ver que cada kernel pesa los puntos de forma distinta. El kernel rectangular le da el mismo peso a todos los puntos dentro del ancho de banda, el triangular le da más peso a los puntos que están cerca del umbral y el Epanechnikov es un poco menos águdo que el triangular.
La elección del kernel, al igual que en el caso del ancho de banda, afecta la estimación del LATE.
8.4.4 Ajustes no paramétricos
Finalmente, una alternativa bastante usual es la de estimar el LATE utilizando un ajuste no paramétrico. Esto significa que no vamos a asumir una forma funcional específica para la relación entre la running variable y el outcome. En cambio, vamos a utilizar técnicas como los splines o los Locally estimated/weighted scatterplot smoothing (LOESS) para ajustar una curva a los datos.
Por ejemplo, veamos cómo se ve la estimación del LATE en este caso.
Ver el código
ggplot(tutoring_centered, aes(x = entrance_centered,
y = exit_exam,
color = tutoring,
fill = tutoring)) +
geom_point(size = 1.5, alpha = .3) +
# Agregamos una linea basada en un modelo lineal para la running variable menor a 70
geom_smooth(data = filter(tutoring_centered, tutoring == "Sí")) +
# Agregamos una linea basada en un modelo lineal para la running variable mayor a 70
geom_smooth(data = filter(tutoring_centered, tutoring == "No")) +
# Ponemos una línea vertical en el umbral
geom_vline(xintercept = 0, color = "darkblue", linetype = "dashed") +
# Las lables
labs(x = "Puntaje en el examen de entrada (centrado)",
y = "Puntaje en el examen de salida",
color = "Participó en la tutoría",
fill = "Participó en la tutoría") +
# Colores más chetos
scale_color_brewer(palette = "Dark2") +
scale_fill_brewer(palette = "Dark2") +
# Theme sin fondo gris
theme_minimal() +
theme(legend.position = "top")
#> `geom_smooth()` using method = 'loess' and formula = 'y ~ x'
#> `geom_smooth()` using method = 'loess' and formula = 'y ~ x'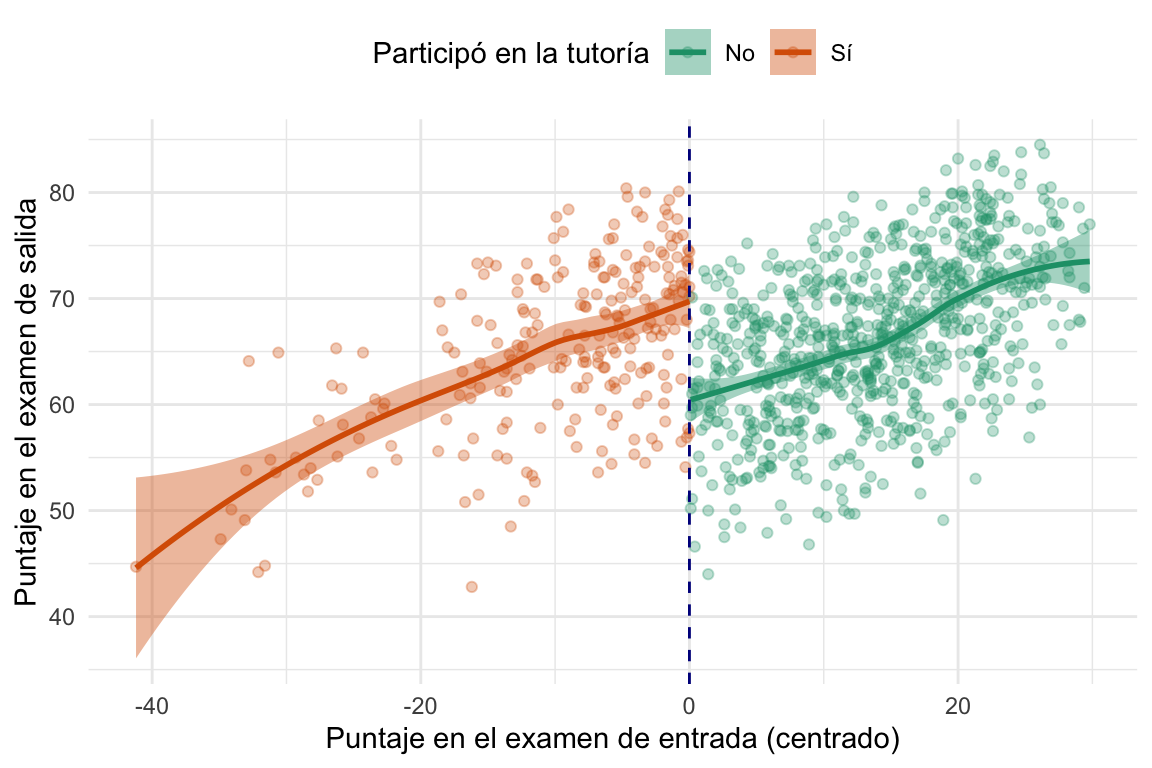
En este caso estamos usando la función de regresión local geom_smooth() de ggplot2 para ajustar una curva a los datos. Esta función utiliza un ajuste LOESS por defecto, pero también podemos especificar otros métodos de ajuste. Podemos ver que no se trata de una curva suave sino más bien de una especie de promedio móvil pesado que va siguiendo a los puntos.
En la estimación no paramétrica como en la paramétrica vamos a calcular el LATE como la diferencia entre las estimaciones del modelo de cada lado del umbral, y como en el caso anterior, la elección del ancho de banda y del kernel afecta la estimación del LATE.
Acá ya no es tan fácil obtener la estimación del efecto ajustando modelos lineales así que vamos a hechar mano de un paquete para esto: rdrobust. Este paquete nos permite ajustar modelos de regresión discontinua de forma sencilla y rápida, y nos da una serie de opciones para ajustar el ancho de banda y el kernel. Empecemos utilizando los valores por defecto.
full <- rdrobust(y = tutoring$exit_exam, x = tutoring$entrance_exam, c = 70)
#> Warning in rdrobust(y = tutoring$exit_exam, x = tutoring$entrance_exam, :
#> Mass points detected in the running variable.
summary(full)
#> Sharp RD estimates using local polynomial regression.
#>
#> Number of Obs. 1000
#> BW type mserd
#> Kernel Triangular
#> VCE method NN
#>
#> Number of Obs. 237 763
#> Eff. Number of Obs. 144 256
#> Order est. (p) 1 1
#> Order bias (q) 2 2
#> BW est. (h) 9.969 9.969
#> BW bias (b) 14.661 14.661
#> rho (h/b) 0.680 0.680
#> Unique Obs. 155 262
#>
#> =============================================================================
#> Method Coef. Std. Err. z P>|z| [ 95% C.I. ]
#> =============================================================================
#> Conventional -8.578 1.601 -5.359 0.000 [-11.715 , -5.441]
#> Robust - - -4.352 0.000 [-12.101 , -4.587]
#> =============================================================================Vemos que hay mucha información, como el kernel (triangular), el ancho de banda (\(9.969\))10, el número de observaciones, etc. Más interesante, al final podemos ver la estimación del LATE que en este caso, el LATE es de 8.6 puntos.
10 La estimación del ancho de banda utiliza un algoritmo data-drive al que no vamos a entrar en detalle, pero que se basa en la idea de que el ancho de banda óptimo es aquel que minimiza el error cuadrático medio de la estimación del LATE. Si quieren ver más detalles pueden consultar la documentación del paquete rdrobust.
Vamos a ver el ajuste qué pinta tiene utilizando la función rdplot() del mismo paquete. Esta función nos permite visualizar el ajuste de la regresión discontinua y ver cómo se ve la estimación del LATE.
Ver el código
rdplot(y = tutoring$exit_exam, x = tutoring$entrance_exam, c = 70)
#> [1] "Mass points detected in the running variable."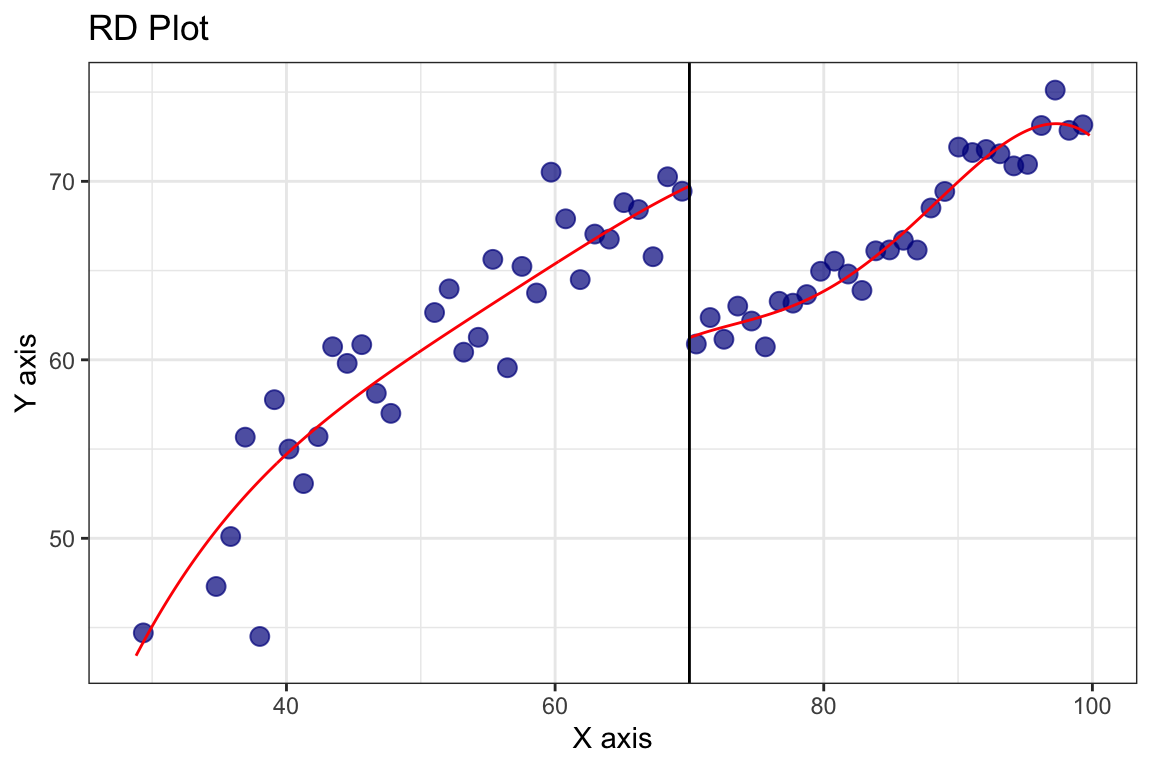
¿Cómo cambia esta estimación si duplicamos el ancho de banda?
Ver el código
doble <- rdrobust(y = tutoring$exit_exam, x = tutoring$entrance_exam, c = 70, h = 9.969 * 2)
rdplot(y = tutoring$exit_exam, x = tutoring$entrance_exam, c = 70, h = 2*9.969)
#> [1] "Mass points detected in the running variable."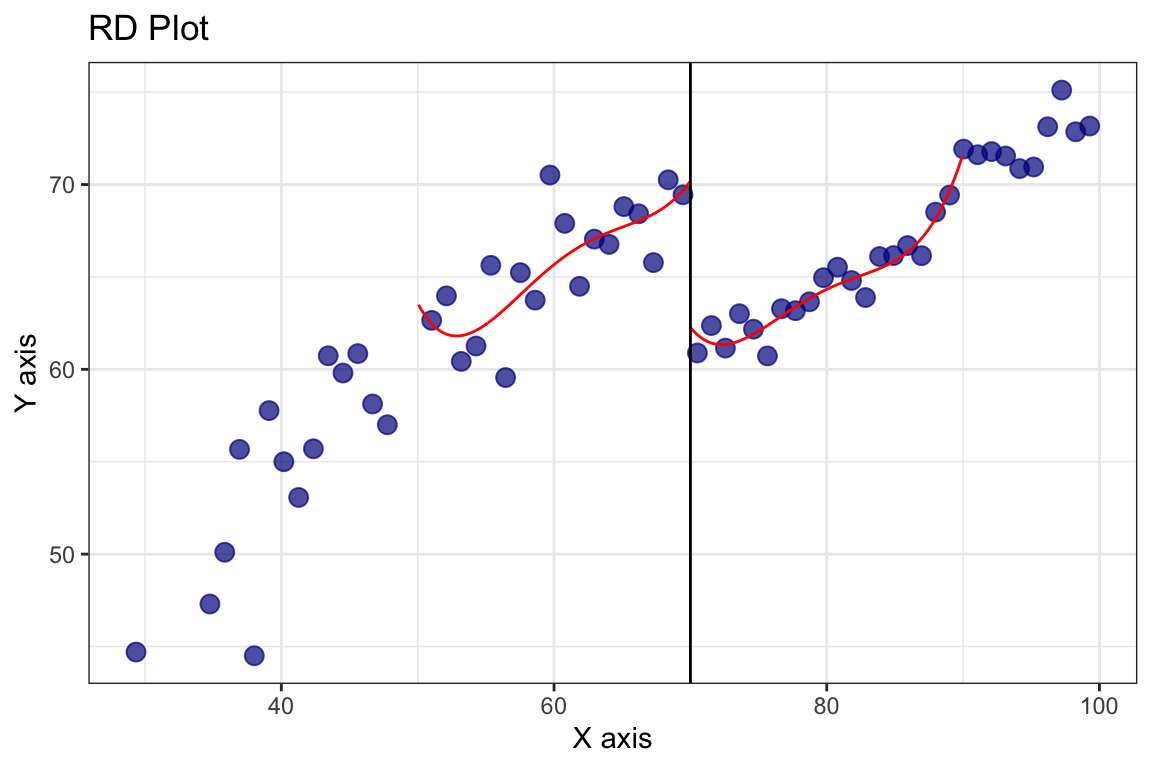
Veamos las estimaciones del LATE para el ancho de banda completo, el doble y la mitad del ancho de banda estimado.
Ver el código
# Un approach posible es usar el recomendado, el doble y la mitad
mitad <- rdrobust(y = tutoring$exit_exam, x = tutoring$entrance_exam, c = 70, h = 9.969 * 0.5)
tibble(BW = c("Full = 9.97", "Doble = 19.94", "Mitad = 4.99"),
Estimate = -round(c(full$Estimate[1], doble$Estimate[1], mitad$Estimate[1]), 3)) |>
gt()| BW | Estimate |
|---|---|
| Full = 9.97 | 8.578 |
| Doble = 19.94 | 9.151 |
| Mitad = 4.99 | 8.201 |
Si bien hay diferencias, podemos ver que la estimación es bastante consistente, algo que es deseable y que nos indica que, al menos en esa región, el efecto es relativamente constante.
Algo que podemos modificar también es el kernel utilizado. Cambiemos de triangular a uniforme y veamos el ajuste.
Ver el código
rdplot(y = tutoring$exit_exam, x = tutoring$entrance_exam, c = 70, h = 9.969, kernel = "uniform")
#> [1] "Mass points detected in the running variable."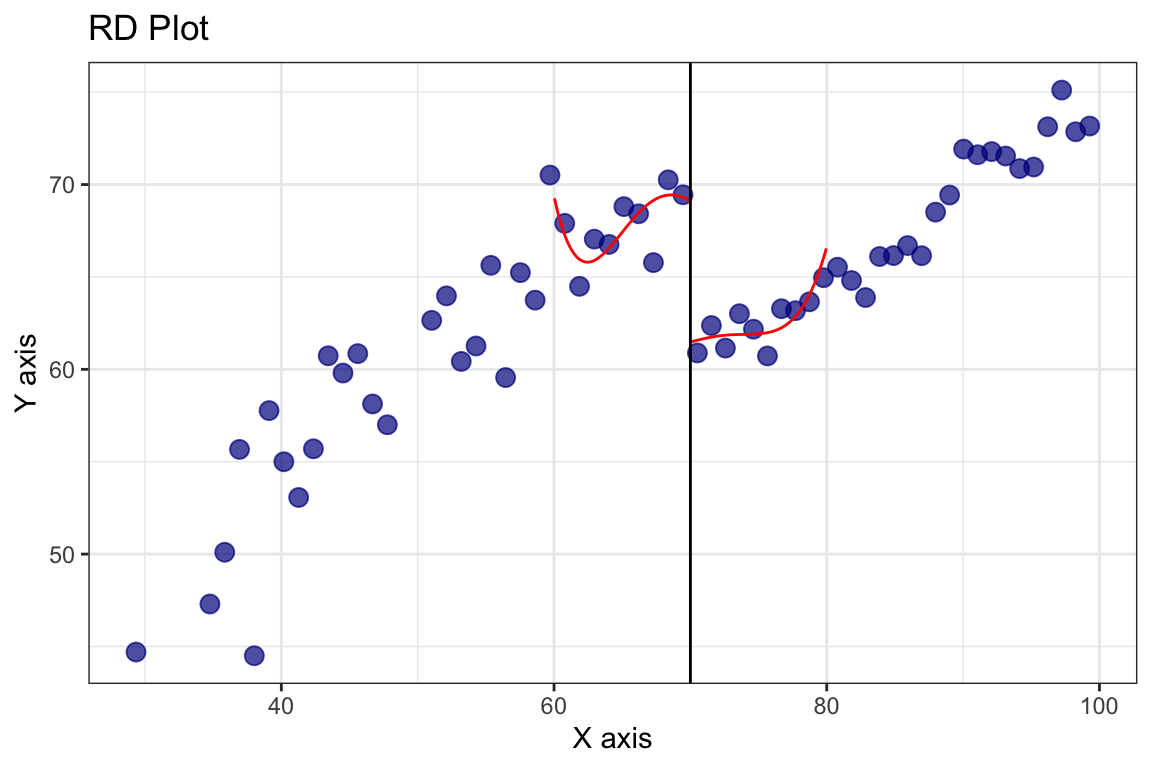
Y veamos cómo esta elección afecta a la estimación del LATE.
Ver el código
triangular <- rdrobust(y = tutoring$exit_exam, x = tutoring$entrance_exam, c = 70, kernel = "triangular")
#> Warning in rdrobust(y = tutoring$exit_exam, x = tutoring$entrance_exam, :
#> Mass points detected in the running variable.
epanechnikov <- rdrobust(y = tutoring$exit_exam, x = tutoring$entrance_exam, c = 70, kernel = "epanechnikov")
#> Warning in rdrobust(y = tutoring$exit_exam, x = tutoring$entrance_exam, :
#> Mass points detected in the running variable.
uniforme <- rdrobust(y = tutoring$exit_exam, x = tutoring$entrance_exam, c = 70, kernel = "uniform")
#> Warning in rdrobust(y = tutoring$exit_exam, x = tutoring$entrance_exam, :
#> Mass points detected in the running variable.
tibble(Kernel = c("Triangular", "Epanechnikov", "Uniforme"),
Estimate = -round(c(triangular$Estimate[1], epanechnikov$Estimate[1], uniforme$Estimate[1]), 3)) |>
gt()| Kernel | Estimate |
|---|---|
| Triangular | 8.578 |
| Epanechnikov | 8.389 |
| Uniforme | 8.175 |
De nuevo, vemos que no hay grandes cambios.
8.4.5 ¿Cómo tomamos decisiones?
Creo que de la sección anterior ya queda un poco claro cómo es la mano: Hay que probar y ver que pasa. Es muy importante que las estimaciones del LATE sean robustas a las decisiones que tomamos. Por ejemplo, si al cambiar el ancho de banda o el kernel la estimación del LATE cambia drásticamente, entonces tenemos que pensar por qué y justificar nuestra elección. Si, por el contrario, la estimación es bastante consistente, entonces podemos estar más tranquilos.
Miremos que hacen, por ejemplo, en Schafer y Holbein (2020). En la siguiente figura se estima el efecto para distintos valores de la running variable (en este caso, la diferencia de horas entre el horario de verano y el horario estándar) y se ve que la estimación del LATE es bastante consistente11.
11 BONUS: ¿Por qué creen que la estimación del ancho de banda más chico tiene el error más grande?
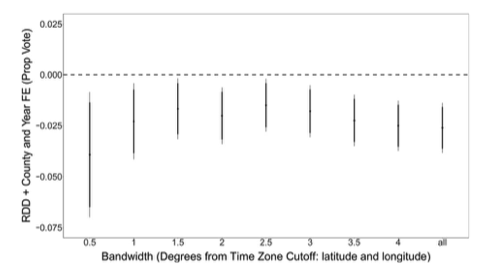
En nuestro ejemplo de juguete podemos hacer algo parecido, comparar todas las estimaciones que fuimos haciendo a lo largo del capítulo:
Ver el código
tabla_results <- tibble(Método = c(rep("Paramétrico", 3), rep("No paramétrico", 5)),
Kernel = c(rep("No pesado",3), rep("Triangular",3), "Epanechnikov", "Uniforme"),
BW = c("Full", 10, 5, round(c(full$bws[1,1], doble$bws[1,1], mitad$bws[1,1], epanechnikov$bws[1,1], uniforme$bws[1,1]), 3)),
Estimate = round(c(modelo_lm$coefficients[3], model_bw_10$coefficients[3], model_bw_5$coefficients[3],
-full$Estimate[1], -doble$Estimate[1], -mitad$Estimate[1], -epanechnikov$Estimate[1], -uniforme$Estimate[1]), 3))
tabla_results |>
gt() |>
gt_highlight_rows(rows = 4,
fill = "lightyellow",
font_weight = "bold")| Método | Kernel | BW | Estimate |
|---|---|---|---|
| Paramétrico | No pesado | Full | 10.800 |
| Paramétrico | No pesado | 10 | 9.273 |
| Paramétrico | No pesado | 5 | 9.122 |
| No paramétrico | Triangular | 9.969 | 8.578 |
| No paramétrico | Triangular | 19.938 | 9.151 |
| No paramétrico | Triangular | 4.984 | 8.201 |
| No paramétrico | Epanechnikov | 8.201 | 8.389 |
| No paramétrico | Uniforme | 7.346 | 8.175 |
Vemos que, en general, no hay grandes diferencias entre las estimaciones del efecto. La línea resaltada es tal vez el efecto que elegiría si tuviera que quedarme con uno, ya que el ancho de banda está elegido basado en los datos, el ajuste es no paramétrico y el kernel le da más importancia a los datos cerca del umbral. Pero, como vimos en Schafer y Holbein (2020), tal vez sea una buena idea presentar todas las estimaciones y discutirlas.
8.5 Limitaciones de la regresión discontinua
La regresión discontinua es una herramienta muy interesante y con mucho auge en la investigación causal, especialmente cuando tenemos confusores no observados. Pero, como vimos, requiere de algunas condiciones particulares para poder aplicarla: tener una running variable que sea continua y que tenga un umbral, y que los sujetos a uno y otro lado del umbral sean comparables (ya vamos a hablar un poco de esto). En esta sección vamos a nombrar brevemente tres de las pincipales limitacinoes de la regresión discontinua.
8.5.1 Es data greedy
Una de las principales limitaciones de la regresión discontinua es que requiere una gran cantidad de datos para poder estimar el efecto causal. Esto se debe a que los sujetos que son comparables para una estimación confiables del LATE son aquellos que están cerca del umbral. Por lo tanto, nuestra muestra puede ser grande, pero una vez que fijamos el ancho de banda se puede reducir notablemente.
8.5.2 Es limitada en alcance
Otra limitación de la regresión discontinua es que el efecto estimado es local, es decir, sólo es válido para los sujetos que están cerca del umbral. Esto significa que no debemos generalizar esta estimación a toda la población, es decir, tenemos un problema de validez externa. Esto podría ser un problema ya que normalmente queremos estimar el efecto para la población de interés.
Acá cabe una breve reflexión: ¿No son todos los efectos que calculamos de algún modo locales? Entonces, resulta interesante pensar cuáles son las condiciones necesarias para que el LATE estimado sea generalizable. Por ejemplo: ¿Creen que el ejemplo del padrón electoral es generalizable? Cada problema se enfrenta con esa pregunta y cada respuesta requiere de un conocimiento del dominio y de la muestra con la que se está trabajando para responderla.
8.5.3 Puede haber problemas de manipulación
Recordemos algo: Al asumir que los participantes de un lado y del otro de la discontinuidad son comparables, estamos asumiendo que hay continuidad en la esperanza de los potential outcomes, es decir, que si un sujeto estuviera en el grupo tratamiento tendría en el umbral el mismo outcome que tendría un miembro del grupo control si hubiera sido asignado al tratamiento. Es un trabalenguas, ¿no? Veamos primero las cuentas y pensemos después en un ejemplo.
Con continuidad de los potential outcomes nos referimos a que los potential outcomes no cambian abruptamente en el umbral, es decir, que la esperanza de los potential outcomes es continua en el umbral. En difícil: que \(E[Y_i^1]\) y \(E[Y_i^0]\) son continuas en el umbral. En términos de la running variable \(X\) y siendo su umbral \(c\), esto significa que:
\[ \begin{align*} \lim_{x \to c^-} E[Y_i^1] = \lim_{x \to c^+} E[Y_i^1] \\ \lim_{x \to c^-} E[Y_i^0] = \lim_{x \to c^+} E[Y_i^0] \end{align*} \]
O gráficamente:
Ver el código
set.seed(123)
data <- tibble(x = runif(200, -10, 10),
y = x + c(rnorm(100, mean = 5, sd = 2),
rnorm(100, mean = 0, sd = 2)),
outcome = c(rep("Y1", 100), rep("Y0", 100))) %>%
mutate(status = if_else((outcome == "Y1" & x>0) | (outcome == "Y0" & x<=0),
"Observable", "Contrafáctico"))
lines <- tibble(intercept = c(5, 0),
slope = c(1, 1),
outcome = c("Y1", "Y0"))
ggplot(data, aes(x = x, y = y, color = outcome)) +
geom_point(aes(alpha = status), size = 2) +
geom_vline(xintercept = 0, linetype = "dashed", color = "darkblue") +
geom_abline(data = lines, aes(slope = slope, intercept = intercept, color = outcome), linewidth = 1) +
labs(x = "Running variable (X)",
y = "Potential outcomes (Y)",
color = NULL,
alpha = NULL) +
scale_color_brewer(palette = "Dark2") +
scale_alpha_manual(values = c(.2, 1)) +
theme_minimal() +
theme(legend.position = "top", legend.box="vertical")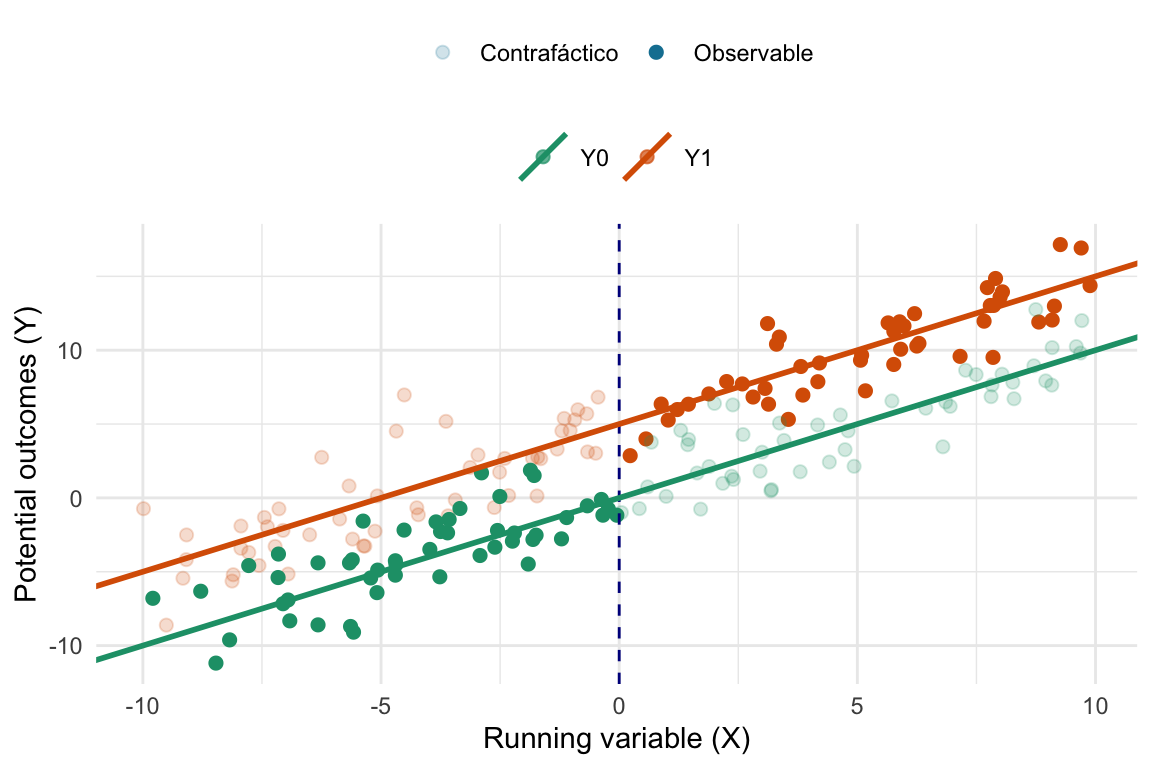
En esta figura vemos como puntos llenos a los observables y como puntos grisados a los contrafácticos, las líneas, son las esperanzas de estos outcomes. Lo que nos interesa pensar es que, si bien en los datos observados vemos un salto al cruzar el umbral (es decir, al pasar de no estar expuesto a estar expuesto al tratamiento), si pudiéramos observar los potential outcomes al cruzar el umbral veríamos que son continuos. Es decir, que si un sujeto estuviera en el grupo tratamiento tendría en el umbral el mismo outcome que que tendría un miembro del grupo control si hubiera sido asignado al tratamiento.
Pensemos qué implicancias tiene esto. Esto significa que la running variable no puede ser manipulada por los sujetos. Es decir, que los sujetos no pueden elegir estar a un lado o del otro del umbral. Por ejemplo, si por algún motivo en nuestro ejemplo los alumnos conocieran la regla de selección y se sacaran peor nota para tener una tutoría gratuita, en ese caso estaríamos hablando de manipulación y la estimación del efecto del tratamiento estaría sesgada.
Vamos con un ejemplo bien concreto. Imaginemos que queremos evaluar la política pública de la que hablamos al principio del capítulo, esa a la que uno califica por cobrar menos de $\(350000\) mensuales. Imaginen que soy un cuentapropista que tengo ese beneficio y a dos días de terminar el mes ya facturé $\(349999\). De golpe me llaman para ofrecerme un trabajo de $\(500\), ¿qué creen que voy a decir? Bueno, si la política es lo suficientemente beneficiosa (más que $\(499\)) probablemente voy a decir que no. ¿Por qué? Porque si acepto el trabajo, voy a perder el beneficio de la política pública. Entonces, en este caso, la running variable (mi ingreso mensual) fue manipulado y, por lo tanto, la continuidad de los potential outcomes no se cumple. Sé que es un ejemplo un poco irreal, pero tómense el tiempo de pensar cuántas veces podemos ver este tipo de manipulación en la vida real.
Existen diversas formas de detectar la manipulación en los datos. Una de las más comunes es la de observar la densidad de la running variable alrededor del umbral. Si hay manipulación, deberíamos ver un salto en la densidad de la running variable en el umbral. Esto se debe a que los sujetos que están cerca del umbral son los que tienen más probabilidades de ser manipulados. Existe algo llamado test de densidad de McCrary que sirve para verificar esto (McCrary (2008)), pero no vamos a entrar en demasiado detalle. Este test está implementado en la función rddensity() del paquete rddensity.
Veamos cómo se ve la densidad de la running variable en nuestro ejemplo de las tutorías (utilizando las funciones rddensity y rdplotdensity).
Ver el código
test_density <- rddensity(tutoring$entrance_exam, c = 70)
plot_density_test <- rdplotdensity(rdd = test_density,
X = tutoring$entrance_exam,
type = "both")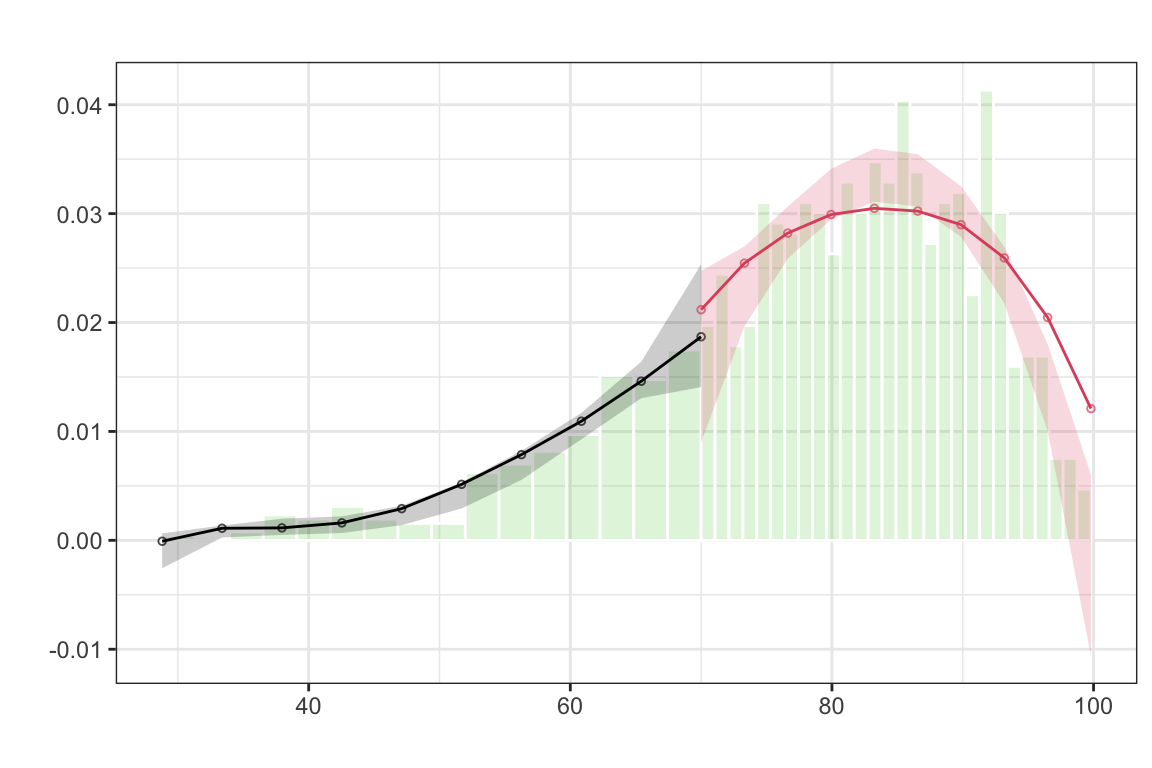
Es razonable decir que no hay manipulación ¿no?