3 Potential outcomes
3.1 Guerra fría, manos y contrafácticos.
Son las 3 de la mañana del 26 de septiembre de 1983. Con una taza de café en mano, Stanislav Petrov vigila las alarmas de una estación de monitoreo de ataques nucleares a las afueras de Moscú. De pronto, los paneles se iluminan con un rojo furioso: tres misiles intercontinentales están en camino a la cúpula del Kremlin… o, quizás, el sistema tiene un error y se trata de una falsa alarma.
Stanislav no duda. Sigue el protocolo y llama al Kremlin. En menos de tres minutos, Rusia lanza un ataque nuclear contra las principales ciudades de EE. UU. La contrarespuesta estadounidense borra Leningrado y Stalingrado unos 40 minutos después. Además de millones de muertos, los ataques levantan tal cantidad de polvo en la atmósfera que el mundo se sume en un invierno nuclear durante 30 años, provocando hambruna en gran parte del hemisferio norte. Menos afectada por los ataques, la economía africana mejora lentamente y se convierte en el principal proveedor de alimentos del mundo. Para 2025, el Imperio Panafricano es la principal potencia económica global.
Todos sabemos que esto nunca ocurrió. Lo que realmente pasó fue que Stanislav Petrov pensó que se trataba de un error y nunca avisó a nadie (pueden ver la historia aquí).
Este mundo posnuclear es un mundo donde los hechos ocurrieron de manera completamente distinta: un mundo alternativo, un what if, un escenario contrafáctico. Podemos especular sobre lo que habría sucedido si los eventos se hubieran desarrollado de otra forma, pero la realidad es que nunca ocurrieron. Por lo tanto, un contrafáctico, aunque posible, es siempre especulativo.
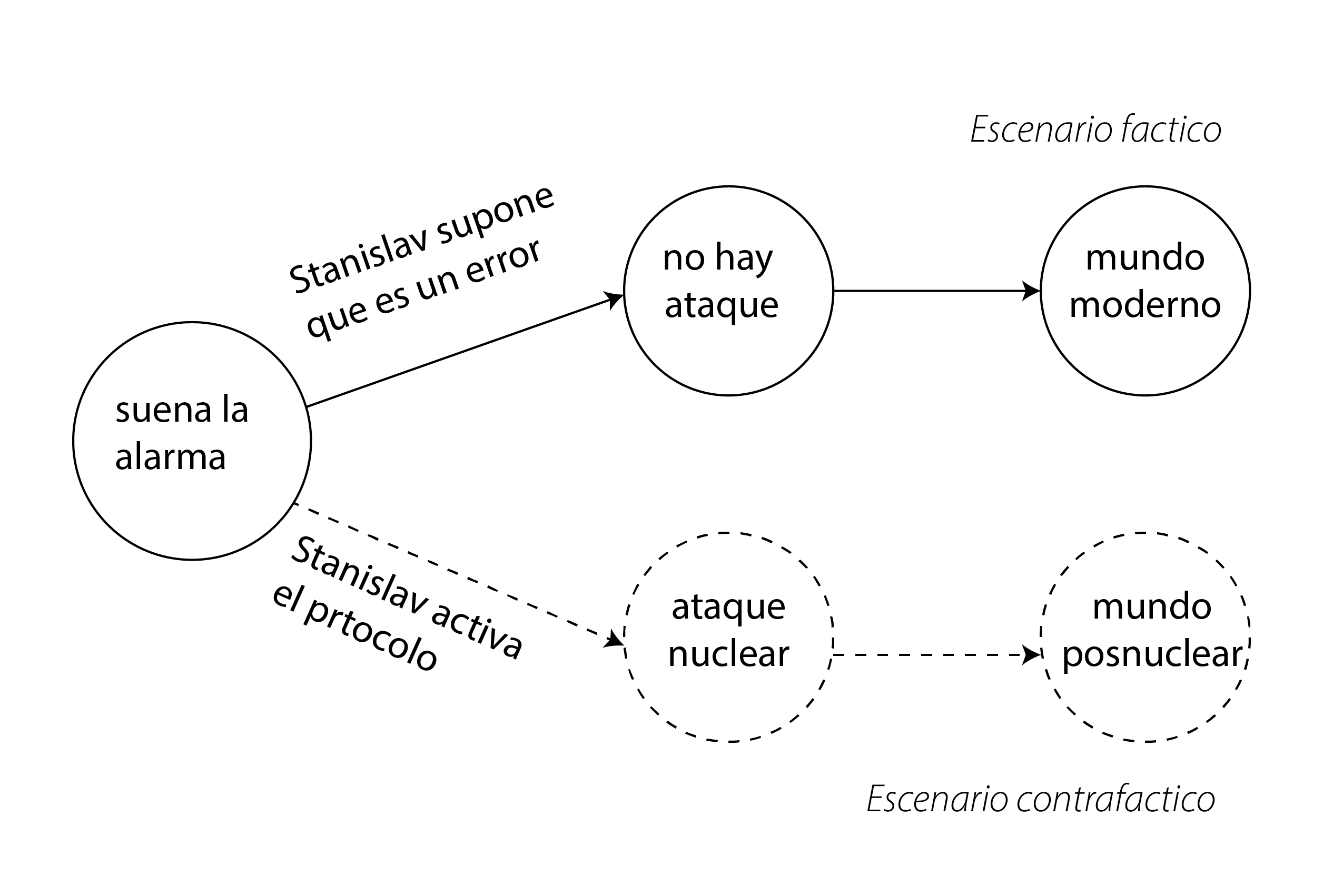
Utilizando el marco conceptual de los potential outcomes de Rubin(Rubin 1974), un contrafactual es el resultado que hubiera ocurrido para una unidad experimental (por ejemplo, una persona, un paciente, un animal de laboratorio o un país) si hubiera recibido un tratamiento diferente del que realmente recibió. Este concepto es fundamental para entender los efectos causales. Nos permite definir lo que entendemos por causa: la diferencia entre lo que realmente sucedió y lo que hubiera sucedido en un escenario alternativo.
En pocas palabras:
Para alguien que recibió el tratamiento, el contrafactual es lo que habría sucedido si no hubiera recibido el tratamiento. Por ejemplo, si un paciente recibió un nuevo medicamento y se recuperó, el resultado contrafactual es su estado de salud si no hubiera recibido el medicamento. Esto nos ayuda a aislar el efecto del medicamento.
Para alguien que no recibió el tratamiento, el contrafactual es lo que hubiera sucedido si hubiera recibido el tratamiento. Por ejemplo, si un estudiante no asistió a un programa de tutoría y reprobó un examen, el contrafactual es su calificación hipotética si hubiera asistido al programa.
Dado que cada unidad recibe solo un tratamiento, solo podemos observar un resultado: el resultado real. El resultado contrafactual es, por definición, inobservable. Esto se conoce a menudo como el problema fundamental de la inferencia causal. Debido a que no podemos observar simultáneamente ambos resultados potenciales para el mismo individuo, vamos a usar métodos y suposiciones estadísticas para estimar los efectos promedio del tratamiento en grupos de individuos. Más de esto en los próximos capítulos.
¿Para qué sirve entonces construir contrafácticos, imaginar cosas que no ocurrieron y que nunca ocurrirán? Veamos otra historia.
Este cuadro que se ve a continuación se llama Praying Hands y fue pintado por Albrecht Durero. Es una de las obras más importantes de su siglo.
Los Durero eran una familia de mineros pobres del sur de Alemania. Dos de sus hijos, Albrecht y Joseph, tenían talento para el dibujo y decidieron hacer un pacto: uno estudiaría en Núremberg durante cuatro años mientras el otro trabajaría en las minas para pagar su educación. Decidirían quién haría qué cosa lanzando una moneda al aire. Pasado ese tiempo, intercambiarían lugares.
El azar favoreció a Albrecht. Durante esos cuatro años, se convirtió en un pintor famoso y regresó a casa para cumplir su parte del acuerdo. Sin embargo, al llegar, Joseph lo recibió con una triste noticia: era demasiado tarde. El arduo trabajo en la mina le había provocado una artritis severa, impidiéndole sostener un pincel. Como único tributo a su sacrificio, Albrecht decidió pintar sus manos.
Ahora tenemos dos escenarios contrafacticos, lo que le hubiera sucedido a Albretch si se quedaba en la mina, y lo que le hubiera sucedido a Joseph si se iba a estudiar a Nuremberg. De modo que el escenario seria asi.
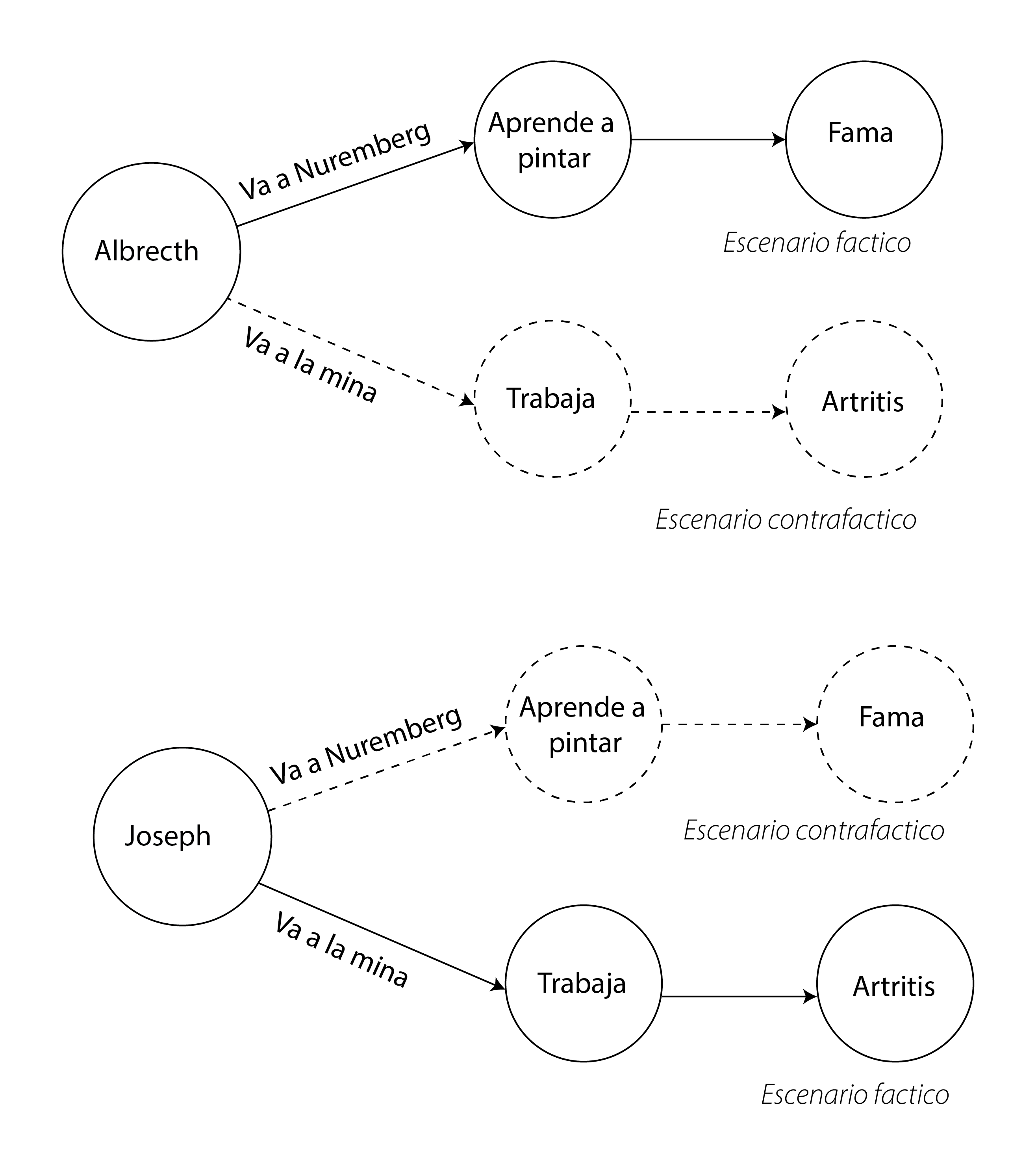
Ambos son hermanos, y uno podría creer que, entre otra cosas, comparten cierto talento y sensibilidad artística. Asimismo, uno podria suponer que el destino de Joseph podría servir para suponer con mayor precisión lo que le paso “le hubiera pasado a Albretch de no ir a Nuremberg” (escenario contrafactico) y el destino de Albetch “lo que le hubiera pasado a Joseph si hubiera podido ir a Nuremberg” (escenario contrafáctico). Entonces imaginar escenarios contrafácticos nos permiten estimar el efecto de ir a Nuremberg o de quedarse.
Ahora bien, es Joseph lo mismo que Albrecth, si la moneda hubiera favorecido a Joseph, ¿habría un Durero pintor famoso? Bueno no estamos seguros de eso, lo que si podemos estar seguros es que pese a parecidos, ellos no son exactamente la misma persona y quizás había diferencias en talentos o en suceptibilidad a la artritis lo que hace que el destino de uno funcione como un símil o proxy de su destino contrafáctico pero no el destino en si mismo. Con estas ideas podemos armar un marco teóprico donde esos efectos se puedan estimar.
Supongamos que quiero evaluar la efectividad de la aspirina para mitigar el dolor de cabeza. Me duele la cabeza y lo quiero es saber el efecto diferencial entre tomar y no tomar esa aspirina. Es decir, en el tiempo 0 estoy yo con dolor de cabeza y en el tiempo 1 debería haber dos versiones mías (como si una no fuera suficiente), la que tomó la aspirina y la que no. A cada una de ellas les tendría que preguntar cuánto les duele la cabeza, el outcome de mi comparación. No hace falta ser demasiado astuto para darse cuenta que esto es imposible ya que sólo nos será posible obsevar una de esas versiones mientras que la otra será un contrafáctico.
De esto vamos a hablar en este capítulo, utilizando como marco teórico a los potential outcomes. Estas ideas terminan de tomar forma en la versión que conocemos en las ciencias sociales propuestas por Rubin(Rubin 1974).
3.2 Potential outcomes
Lo que nos proponen los potential outcomes es la definición del efecto causal como la comparación de dos estados del mundo. En una versión del mundo, la “actual” (u obsevada), me tomo una aspirina y a las dos horas registro la severidad de mi dolor de cabeza mientras que en la otra versión del mundo, la “contrafactual”, no me la tomo y las dos horas registro la severidad del dolor. A partir de esto, la tradición de los potential outcomes define al efecto causal de tomar una aspirina en el dolor de cabeza como la diferencia entre esas dos mediciones.
Todo muy lindo, pero como ya estarán sospechando es imposible calcular un efecto que está expresado en función de un contrafactual, ya que este contrafactual no lo podemos observar. Pero no se preocupen que le vamos a encontrar la vuelta.
Empecemos con un poco de notación que nos va a ayudar a acomodar las ideas. Por simplicidad vamos a asumir una variable binaria para la asignación del grupo experimental (por ejemplo, tratamiento y control). Esta variable vale \(1\) si la unidad i recibe el tratamiento y \(0\) si no, o sea, si pertenece al grupo control. Cada unidad \(i\) va a tener dos potential outcomes: \(Y_i^1\) si la unidad recibió el tratamiento y \(Y_i^0\) si no. Esto significa que una unidad experimental en el mismo momento del tiempo va a recibir y no recibir el tratamiento, o sea, alguno de estos va a ser contrafactual1.
1 De ahí el nombre de potential, porque se trata de posibles estados del mundo. Un estado en el que la unidad \(i\) recibe el tratamiento y uno en el que no.
Los outcomes observables difieren de los potenciales. Los potenciales son variables aleatorias parcialmente latentes — solo uno de sus valores se revela por unidad —, mientras que los observables son sus realizaciones medibles. Hay una ecuación que nos permite definir el outcome observable (\(Y^i\)) en función de los potenciales, se llama la switching equation:
\[ Y_i = D_i Y_i^1 + (1-D_i) Y_i^0 \tag{3.1}\]
Donde \(D_i\) vale \(1\) si la unidad i recibió el tratamiento (entonces \(Y_i=Y_i^1\)) y \(0\) si no (entonces \(Y_i=Y_i^0\)). Vale la pena notar que \(Y_i\), el outcome observable, no tiene ningún supraíndice ya que no es más potencial. Esto tambien es una forma de hacer explicito el problema del outcome observable, porque dependiendo el valor que adopte \(D_i\) uno de los términos se vuelve cero. Si \(D_i=0\), \(Y_i=Y_i^0\) ya que el término \(D_i Y_i^1\) vale 0. Si por el contrario \(D_i=1\), \(Y_i=Y_i^1\) porque el término \((1-D_i) Y_i^0\) vale cero. Esta es una forma sofisticada de decir que el outcome observable sólo es posible en una de las dos formas de \(D_i\).
Usando esta notación definimos el efecto causal del tratamiento para una unidad \(i\) como:
\[ \delta_i = Y_i^1 - Y_i^0 \tag{3.2}\]
Donde queda claro que para estimar el efecto causal de acuerdo a la tradición de los potential outcomes debemos conocer dos estados del mundo a los que es imposible acceder simultáneamente. Y aqui yace el problema funcamental de la inferencia causal: Para calcular el efecto causal se requiere acceso a datos que siempre nos van a faltar: los contrafácticos(Rubin 1974).
3.3 Efecto promedio del tratamiento
Al igual que los potential outcomes, el efecto para la unidad \(i\) (\(\delta_i\)) también es una variable aleatoria, y su esperanza es lo que vamos a llamar el efecto promedio del tratamiento (ATE2). El ATE va a ser la magnitud de interés en nuestros experimentos, el efecto promedio de mi tratamiento. El mismo se define de la siguiente forma:
2 Del inglés Average treatment effect.
\[ \begin{array} _ATE &=& E[\delta_i] \\ &=& E[Y_i^1 - Y_i^0] \\ &=& E[Y_i^1] - E[Y_i^0] \end{array} \tag{3.3}\]
Ahora vamos a definir el efecto promedio, pero para el grupo tratado (es decir, los participantes asignados al grupo tratamiento, con \(D_i=1\)):
\[ \begin{array} _ATT &=& E[\delta_i|D_i=1] \\ &=& E[Y_i^1 - Y_i^0|D_i=1] \\ &=& E[Y_i^1|D_i=1] - E[Y_i^0|D_i=1] \end{array} \tag{3.4}\]
Esta magnitud se llama ATT3 y se calcula de la misma forma que el ATE pero condicionando los \(\delta_i\) al valor de \(D_i\) igual a 1. De manera análoga, definimos el efecto promedio pero para el grupo no tratado4(\(D_i=0\))
3 Del inglés Average treatment effect for the treated.
4 Del inglés Average treatment effect for the untreated.
\[ \begin{array} _ATU &=& E[\delta_i|D_i=0] \\ &=& E[Y_i^1 - Y_i^0|D_i=0] \\ &=& E[Y_i^1|D_i=0] - E[Y_i^0|D_i=0] \end{array} \tag{3.5}\]
Ojo con confundir estos tres conceptos. Creo que el ATE es autoexplicativo, pero se suele confundir ATT y ATU. En el primer caso, el ATT e,s como su nombre lo indica, el efecto promedio del tratamiento para el grupo de tratamiento. Estamos calculando la esperanza de los \(\delta_i\) para los individuos pertenecientes al grupo tratamiento. Esto involucra tanto sus \(Y^1_i\) como sus \(Y^0_i\). En el segundo caso, el ATU es el efecto promedio del tratamiento para el grupo de no tratamiento, es decir, la esperanza de los \(\delta_i\) para los individuos pertenecientes al grupo control.
Es una confusión común confundir estos efectos promedios con magnitudes no potenciales pero, como se observa de sus fórmulas, tanto estos últimos dos como el ATE no se pueden calcular en la práctica.
En las secciones siguientes vamos a ver como, cumpliendo ciertas condiciones5, podemos estimar el ATE a partir de los outcomes observables.
5 Spoiler: Asignación aleatoria de las unidades experimentales a los grupos.
3.4 Diferencia de medias simple
¿Qué es lo que sí podemos observar? Una magnitud que a priori podríamos creer que va a estar relacionada con el ATE y que podemos observar es la diferencia de medias entre los outcomes observados del grupo tratamiento y el grupo control. La vamos a llamar SDO6 y se calcula de la siguiente forma:
6 Del inglés simple difference in outcomes.
\[ \begin{array} _SDO &=& E[Y_i^1|D_i=1] - E[Y_i^0|D_i=0] \\ &=& \frac{1}{N_T} \sum_{i=1}^{N_T} (y_i|d_i=1) - \frac{1}{N_C} \sum_{i=1}^{N_C} (y_i|d_i=0) \end{array} \tag{3.6}\]
Donde \(N_T\) y \(N_C\) son la cantidad de individuos en el grupo tratamiento y control respectivamente (y \(N_T + N_C = n\)). Todo muy lindo, pero operemos un poquito para ver hasta que punto el SDO es un estimador insesgado del ATE. Empecemos escribiendo el ATE como una suma pesada del ATT y el ATU:
\[ \begin{array} _ATE &=& \pi ATT + (1-\pi) ATU \\ &=& \pi E[Y_i^1|D_i=1] - \pi E[Y_i^0|D_i=1] + \\ & & (1-\pi) E[Y_i^1|D_i=0] - (1-\pi) E[Y_i^0|D_i=0] \\ &=& \bigl\{ \pi E[Y_i^1|D_i=1] + (1-\pi) E[Y_i^1|D_i=0] \bigl\} - \\ & & \bigl\{ \pi E[Y_i^0|D_i=1] + (1-\pi) E[Y_i^0|D_i=0] \bigl\} \end{array} \tag{3.7}\]
Con \(\pi = N_T/n\) y \(1 - \pi = N_C/n\). Es decir \(\pi\) es la proporción de individuos tratados y \(1 - \pi\) es la proporción de individuos no tratados.
Operando con la Ecuación 3.7 podemos despejar la diferencia entre los outcomes observables (SDO) y ver cómo esta se relaciona con el resto de las magnitudes definidas7.
7 Pueden ver el despeje numérico en detalle en el capítulo 4 de (Cunningham 2021).
\[ \begin{array} _E[Y_i^1|D_i=1] - E[Y_i^0|D_i=0] &=& ATE \\ &+& ( E[Y_i^0|D_i=1] - E[Y_i^0|D_i=0] ) \\ &+& (1-\pi) (ATT - ATU) \end{array} \]
Que podemos reescribir como:
\[ \begin{array} _\underbrace{\frac{1}{N_T} \sum_{i=1}^{N_T} (y_i|d_i=1) - \frac{1}{N_C} \sum_{i=1}^{N_C} (y_i|d_i=0)}_\text{Diferencia de los outcomes} &=& \underbrace{ATE}_\text{Efecto promedio del tratamiento} \\ &+& \underbrace{( E[Y_i^0|D_i=1] - E[Y_i^0|D_i=0] )}_\text{Sesgo de selección} \\ &+& \underbrace{(1-\pi) (ATT - ATU)}_\text{Sesgo de efecto heterogéneo} \end{array} \tag{3.8}\]
Lo que puede verse en Ecuación 3.8 es que si pudiéramos asegurar de alguna forma que los sesgos de selección y de efecto heterogéneo fueran cero, el SDO sería un buen estimador del ATE que es, al fin y al cabo, el efecto causal promedio que nos interesa en nuestro experimento.
O sea que la clave del diseño experimental va a ser encontrar la forma de asegurar que esos sesgos sean nulos. Veamos mejor que representan para poder entender como minimizarlos.
3.4.1 Sesgo de seleccion
Miremos con detenimiento la formula a la que llamamos sesgo de selección \(E[Y_i^0|D_i=1] - E[Y_i^0|D_i=0]\). Si la definimos a partir de esta ecuacion representa la diferencia entre los dos grupos si nunca hubiera habido un tratamiento en primer lugar. Es decir, son las diferencias inherentes entre los dos grupos. Estas diferencias aparecen al seleccionar individuos en un grupo y no en el otro, por eso lo llamamos sesgo de selección. Por el contrario, mientras mas se parezcan en el outcome \(Y_i^0\) los individuos asignados a uno u otro grupo \(D\), mas cercano a cero será el sesgo de selección. Entonces, sería ideal medir el sesgo de selección ya que es una medida de cuan lejos está el estimador del ATE (el SDO) del verdadero valor. Sin embargo el primer término de la ecuación es un contrafáctico. No nos queda otra alternativa que buscar una condición en donde, aunque no podamos medirlo, podamos confiar en que el sesgo de selección tiene esperanza igual a cero.
3.4.2 Sesgo de tratamiento heterogéneo
Esta tercera componente es un poco más difícil de interpretar, miremoslo bien: \((1-\pi) (ATT - ATU)\). Así definido se puede decir que es la diferencia entre el efecto promedio del tratamiento para el grupo tratamiento (el ATT) y la misma para el grupo control (el ATU) multiplicado por la proporción de sujetos que está en el grupo control. A diferencia del sesgo de selección, en este caso no se trata de una diferencia entre los dos grupos si no hubiera habido tratamiento, sino que es la diferencia entre el efecto del tratamiento para el grupo tratado y el efecto del tratamiento para el grupo control. En otras palabras, este sesgo cuantifica las diferencias en sensibilidad al tratamiento por cada uno de los grupo. Por ejemplo, si estamos testeando una droga para mejorar la resistencia aeróbica y en nuestro grupo tratamiento tenemos a 90% de asmáticos/as mientras que en el grupo control sólo a un 10%, es esperable que los efectos del tratamiento en cada uno de estos grupos sean distintos. Pero ojo, recordamos que ni el ATT y el ATU pueden ser medidos porque incluyen contrafácticos en su definición.
Ahora que entendemos qué representa cada sesgo, podemos buscar una condición en donde la esperanza de ambos sesgos sea igual a 0 para que, de esta forma, el SDO sea finalmente un estimador insesgado del ATE. Esa condicion es la independencia.
3.5 Independencia
La definición de independencia en el contexto de los potential outcomes es la siguiente:
\[ (Y^0, Y^1) \perp D \]
Momento cerebrito, pensemos una poco qué quiere decir. Esto significa que la asignación de los participantes al grupo control o tratamiento (\(D\)) no depende de los outcomes potenciales de ese individuo 8.
8 El símbolo de perpendicularidad quiere simbolizar eso, que no hay relación entre los outcomes potenciales y la asignación a los grupos.
Vamos a pensarlo con un ejemplo concreto. Imaginen que tenemos una grupo de participantes para poner a prueba una cirugía experimental como altenativa a un tratamiento médico establecido no quirúrgico. Si la asingación de individuos al grupo tratamiento la hace un médico en base a lo que cree que va a ser conveniente para él, por ejemplo, no asignando a pacientes de edad avanzada al grupo tratamiento por el riesgo asociado a una cirugía, o asignando a pacientes cuyo pronóstico con el método tradicional vea poco favorable al grupo control. En este caso, la asignación a un grupo sí depende de los posibles resultados, por lo tanto, no hay independencia. Si en lugar de eso tiráramos una moneda antes de recibir a cada paciente, podríamos de esa forma asegurar la independencia.
La independencia implica que se cumpla:
\[ \begin{array} _E[Y^1|D=1] - E[Y^1|D=0] &=& 0 \\ E[Y^0|D=1] - E[Y^0|D=0] &=& 0 \end{array} \tag{3.9}\]
Es decir, que la esperanza de los outcomes para los participantes que fueron asignados tanto al grupo tratamiento como al grupo control serían iguales si pudieramos medirlos a ambos en mundo tratamiento o en mundao control9. Ojo que esto no implica que la esperanza del outcome para tratamiento en los tratados sea igual a la esperanza para no tratamiento en los controles (\(E[Y^1|D=1] - E[Y^0|D=0] = 0\)) ni igual a la esperanza no tratamiento de los tratados (\(E[Y^1|D=1] - E[Y^0|D=1] = 0\)).
9 Tengamos en cuenta que tanto \(E[Y^1|D=0]\) como \(E[Y^0|D=1]\) son escenarios contrafácticos.
¿Qué implicancias tiene las igualdades presentadas en Ecuación 3.9 en los sesgos que vimos en la ecuación Ecuación 3.7? Empecemos por el sesgo de selección (\(E[Y^0|D=1] + E[Y^0|D=0]\)). Vemos que, de acuerdo a la primera línea de Ecuación 3.9, de ser independiente la asignación del grupo experimental, este sesgo sería cero. Pensemos un poco. Lo que nos está diciendo la condición de independencia es que si ambos grupos fueran no tratados, ambos tendrían el mismo outcome lo que pareciera indicarnos que es razonable considerar nulo al sesgo de selección.
La relación del sesgo de efecto heterogéneo (\((1-\pi) (ATT - ATU)\)) con la independencia es un poquito más difícil de demostrar. Olvidémonos del \((1-\pi)\) por un momento. Reescribamos los efectos ATT y ATU:
\[ \begin{array} _ATT &=& E[Y^1|D=1] - E[Y^0|D=1] \\ ATU &=& E[Y^1|D=0] - E[Y^0|D=0] \end{array} \]
Y ahora restemos ambos términos:
\[ \begin{array} _ATT - ATU &=& E[Y^1|D=1] - E[Y^0|D=1] - ( E[Y^1|D=0] - E[Y^0|D=0] )\\ &=& \bigl\{ E[Y^1|D=1] - E[Y^1|D=0] \bigl\} + \bigl\{ E[Y^0|D=0] - E[Y^0|D=1] \bigl\} \end{array} \tag{3.10}\]
Reescrito de esta forma podemos ver los dos primero términos de Ecuación 3.10 se hacen cero por la primera línea de Ecuación 3.9, y los últimos dos se hacen cero por la segunda.
Finalmente, demostramos que si hay independencia en la asignación de los grupos, la diferencia de las medias simple (SDO) entre el grupo tratado y el grupo control es un estimador insesgado del ATE.
3.6 SUTVA
En este capítulo hemos presentado un marco teórico para definir un efecto causal. A ese efecto causal lo llamamos ATE y vimos que es imposible calcularlo por la existencia de contrafácticos pero que puede ser estimado por una medida observable, la SDO. También vimos que SDO contiene al ATE y a un par de sesgos, sesgos que deberían hacerse cero si el supuesto de independencia se cumple.
¿Podría pasar que un efecto causal no pueda ser estimado con este marco teórico? Sí, hay un límite a este marco en donde todas estos cáclulos (medibles o no) son posibles. Si vamos al corazón mismo de todos los cálculos la condición que debe cumplirse para que todo sea posible es que las \(Y_i\) sean restables, en otras palabras que representen lo mismo. A este supuesto se lo llama SUTVA que es la abreviatura de stable unit treatment value assumption. Vamos a reformularlo, SUTVA implica que cada unidad \(i\) recibe la misma dosis de tratamiento.
El SUTVA se cumple siempre que cuando se expone un individuo a un tratamiento; su respuesta sea la misma: 1) Sin importar cómo el participante fue asignado al tratamiento y 2) Sin importar los tratamientos recibidos por las otras unidades.
Sin embargo, en la práctica estos supuestos pueden fallar. En particular, la segunda condición —la ausencia de interferencia entre unidades— puede violarse por fenómenos sociales, conductuales o institucionales que modifican la respuesta de los individuos en función de lo que ocurre con otros. Algunos ejemplos clásicos de estas violaciones son la rivalidad compensatoria, la desmoralización resentida, la difusión o imitación de tratamientos y la ecualización compensatoria de tratamientos.
La rivalidad compensatoria ocurre cuando los individuos del grupo control, al saber (o sospechar) que no están recibiendo el tratamiento, reaccionan esforzándose más para “compensar” esa desventaja. Por ejemplo, en un estudio educativo, los estudiantes que no reciben una nueva intervención pedagógica podrían estudiar más por su cuenta para no quedar atrás. Esto genera que sus resultados mejoren artificialmente, reduciendo la diferencia observada entre tratamiento y control, y por lo tanto subestimando el efecto causal real. En notación de potential outcomes, esto se traduce en que el resultado observable (\(Y_i^0|D_i=0\)) tiene agregado un efecto “compensatorio” que lo hace más grande que su contrafáctico (\(Y_i^0|D_i=1\)), o sea, la respuesta al no-tratamiento en el grupo tratamiento.
En contraste, la desmoralización resentida aparece cuando los individuos del grupo control, al percibirse en desventaja, se desmotivan o reducen su esfuerzo. Siguiendo el mismo ejemplo, estudiantes que no reciben la intervención podrían perder interés o sentirse injustamente tratados, empeorando su desempeño. En este caso, la diferencia entre los grupos se amplifica, lo que puede llevar a sobreestimar el efecto del tratamiento.
La difusión o imitación de tratamientos (también conocida como spillover) ocurre cuando el tratamiento asignado al grupo tratado se filtra hacia el grupo control. Esto puede suceder, por ejemplo, si los participantes comparten información, prácticas o recursos. Como resultado, algunos individuos del grupo control terminan recibiendo, total o parcialmente, el tratamiento, lo que reduce la diferencia entre grupos y tiende a sesgar la estimación hacia cero. En este escenario vuelve a pasar que \(Y_i^0|D_i=0\) tiene un efecto agregado (el tratamiento que se derramo en el sujeto) que lo aleja del contrafáctico \(Y_i^0|D_i=1\). Por ejemplo, si la intervención del ejemplo anterior es el uso de una tablet por parte de los estudiantes, y asignamos a un estudiantes al grupo tratamiento y a su compañero de banco al grupo control, resulta razonable pensar que parte de los beneficios de utilizar dispositivos digitales en el aprendizaje llegue al compañero de banco no tratado.
Finalmente, la ecualización compensatoria de tratamientos se da cuando quienes administran el estudio (docentes, médicos, coordinadores, etc.) otorgan recursos adicionales al grupo control para compensar la falta de tratamiento. Por ejemplo, un docente podría dedicar más tiempo o atención a los estudiantes del grupo control para “equilibrar” la situación. Esto también reduce artificialmente las diferencias entre grupos y dificulta identificar el efecto causal puro del tratamiento. En el ejemplo anterior, si la maestra pasa más tiempo asistiendo al estudiante que no tiene tablet, es probable que este, perteneciente al grupo control termine recibiendo un beneficio adicional que lo aleja de su contrafáctico \(Y_i^0|D_i=1\).
Todos estos fenómenos violan SUTVA porque los resultados de una unidad ya no dependen únicamente de su propio tratamiento, sino también de lo que reciben o hacen otros, o incluso de cómo los administradores reaccionan a la asignación. En otras palabras, los resultados potenciales dejan de ser “estables” y comparables, comprometiendo la validez de nuestras estimaciones causales.
3.7 Preguntas de repaso
Explicá con tus palaras qué es un contrafáctico.
Definí el efecto causal individual (\(\delta_i\)) con el marco teórico de los potential outcomes. ¿Por qué este efecto es, en la práctica, imposible de calcular? ¿Cómo se suele llamar a este problema?
Una persona recibe un tratamiento para la osteoporosis y observás que mejora. ¿Qué datos tendrías que comparar para saber el efecto real del tratamiento en esa persona? ¿Por qué es un problema?
Explicá la switching equation. ¿Qué representa cada término? ¿Por qué es útil esta notación para hacer explícito el problema de la inferencia causal?
¿Qué es el ATE? ¿Qué es el ATT? ¿Qué es el ATU? ¿En qué se diferencian? ¿Pueden calcularse directamente a partir de los datos observados?
¿Qué es el SDO? ¿Bajo que condiciones es un buen estimador del ATE? Recordá la descomposicón del SDO en sus tres componentes y explicá qué representa cada uno.
Estás estudiando el efecto de un dispositivo para la hipoacusia sobre la audición. Sabes que en general las personas con menos síntomas tienden a usar menos el dispositivo. Además, observás que en promedio las personas que no usan el dispositivo tienen mejores resultados que los que sí lo usan.
- ¿Qué estás calculando al comparar los promedios observados entre quienes usan y no usan el dispositivo?
- ¿Eso coincide necesariamente con el ATE?¿Por qué?
- A partir de esta información, ¿Podés concluir que el dispositivo empeora la audición?¿Por qué?
¿Qué es el sesgo de selección? ¿De dónde surge? ¿Bajo que condiciones podemos decir que vale cero?
¿Qué es el sesgo de efecto heterogéneo? ¿Se te ocurre un ejemplo donde podría haber sesgo de efectoi heterogéneo?
¿Qué significa que la asignación al tratamiento sea independiente de los potential outcomes? Escribí formalmente la condición de independencia y explicá sus implicancias para los sesgos del SDO.
¿Cómo la independencia garantiza que el SDO sea un estimador insesgado del ATE? Explicá el argumento tanto para el sesgo de selección como para el sesgo de efecto heterogéneo.
¿Qué es el SUTVA? ¿Cuáles son sus dos condiciones? ¿Por qué es necesario que se cumpla para que el marco de potential outcomes funcione?
¿Cuál es la diferencia entre un crossover y un spillover? ¿Cuál de los dos viola el SUTVA? ¿Por qué?
Estás estudiado el efecto de una intervención para aumentar la seguridad psicológica en un equipo específico de una empresa. Sabes que muchos de los empleados hablan regularmente con los empleados de otro equipo, el cual estas usando como grupo control. Sabes que pueden pasar los siguientes tres casos:
- Los empleados del otro equipo control empiezan a imitar a los de el equipo en el cual estás empleando la intervención
- Los empleados del equipo control ven que están en desventaja y se desmotivan
- Los empleados del equipo control se esfuerzan más en aumentar la seguridad psicológica.
Para cada caso: a) Explica qué es lo que está ocurriendo y como se llama el fenómeno. b) Explica cómo esto puede afectar la estimación del efecto de la intervención
3.8 Un caso aplicado para pensar
El Ministerio de Educación lanzó un programa de tutorías individuales para estudiantes de primer año de secundaria identificados como “en riesgo de abandono” según su desempeño en el último trimestre de primaria. El programa consiste en sesiones semanales con un tutor durante todo el año. Al finalizar el año, se mide el outcome principal: si el estudiante aprobó todas las materias o no (variable binaria, 1=aprobo todas las materias, 0=no aprobó todas las materias).
El programa no fue asignado aleatoriamente: los directores de cada escuela seleccionaron a los estudiantes que consideraron más necesitados, en donde se priorizo a aquellos con peores notas y mayor ausentismo.
Se observa lo siguiente en los datos:
Los estudiantes que participaron del programa tienen una tasa de aprobación del 61%.
Los estudiantes que no participaron tienen una tasa de aprobación del 74%.
Un análisis más detallado muestra que los estudiantes seleccionados para el programa tenían, en promedio, \(3.2\) inasistencias más por mes que los no seleccionados, antes de que el programa comenzara.
Con estos datos, respondé las siguientes preguntas:
Un funcionario concluye: “el programa no funciona, los que participaron aprueban menos que los que no participaron.” ¿Qué magnitud está calculando el funcionario? ¿Es eso el ATE? ¿Por qué sí o por qué no?
Para cada estudiante que participó del programa, ¿cuál sería su resultado contrafactual? ¿Por qué es imposible calcularlo directamente? ¿Cómo se llama este problema?
Identificá y explicá los sesgos presentes en la comparación que hace el funcionario. ¿Qué dice el dato de las \(3.2\) inasistencias al respecto?
Un colega propone usar como grupo control a los estudiantes de otra escuela del mismo barrio que no tiene el programa. Otro colega propone tirar una moneda para asignar quién entra al programa. ¿Cuál de las dos propuestas resolvería mejor el problema identificado en la pregunta anterior? ¿Por qué? Usá el concepto de independencia en tu respuesta.
En la escuela donde se implementa el programa, varios tutores comentan que los estudiantes del grupo control (los que no entraron al programa) empezaron a juntarse con los que sí participan y a recibir consejos de ellos. ¿Qué supuesto del marco de potential outcomes se estaría violando? ¿Cómo afecta esto a la estimación del efecto?