4 Grafos acíclicos dirigidos (DAGS)
Los grafos acíclicos dirigidos 1son una herramienta para representar visualmente las relaciones causales presentes en nuestro diseño experimental, ni más ni menos. Los mismos nos permiten poner en una representación gráfica el conocimiento que tenemos de las variables aleatorias involucradas en un proceso que queremos estudiar y las relaciones causales entre ellas. Además, existen herramientas que, a partir de características de los DAGS, nos permiten decidir cuál es el modelo estadístico cuyo parámetro será una estimación del efecto causal que queremos estudiar.
1 A partir de ahora DAGS, del inglés Directed acyclic graphs.
4.1 Definiciones, características y ejemplos
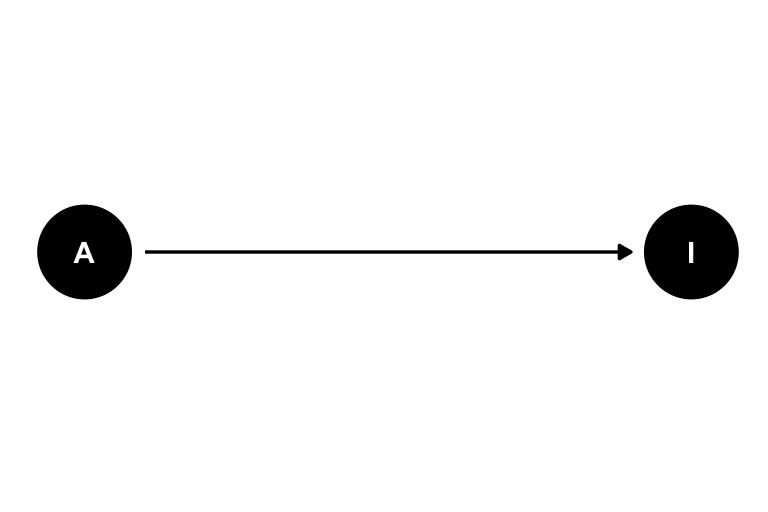
Un DAG es una representación gráfica de una cadena de efectos causales. Los nodos (los circulitos o cuadraditos que vamos a ver más adelante) representan variables aleatorias y las flechas que los unen representan la relación causal que se mueve de una variable a la otra en la dirección intuitiva de la flecha. Por ejemplo, pensemos que queremos estudiar el efecto de tomar una aspirina en la intensidad de nuestro dolor de cabeza cuando nos duele la cabeza. Tenemos dos variables Aspirina (A) e Intensidad del dolor (I). Esta relación la podemos expresar en el siguiente DAG:
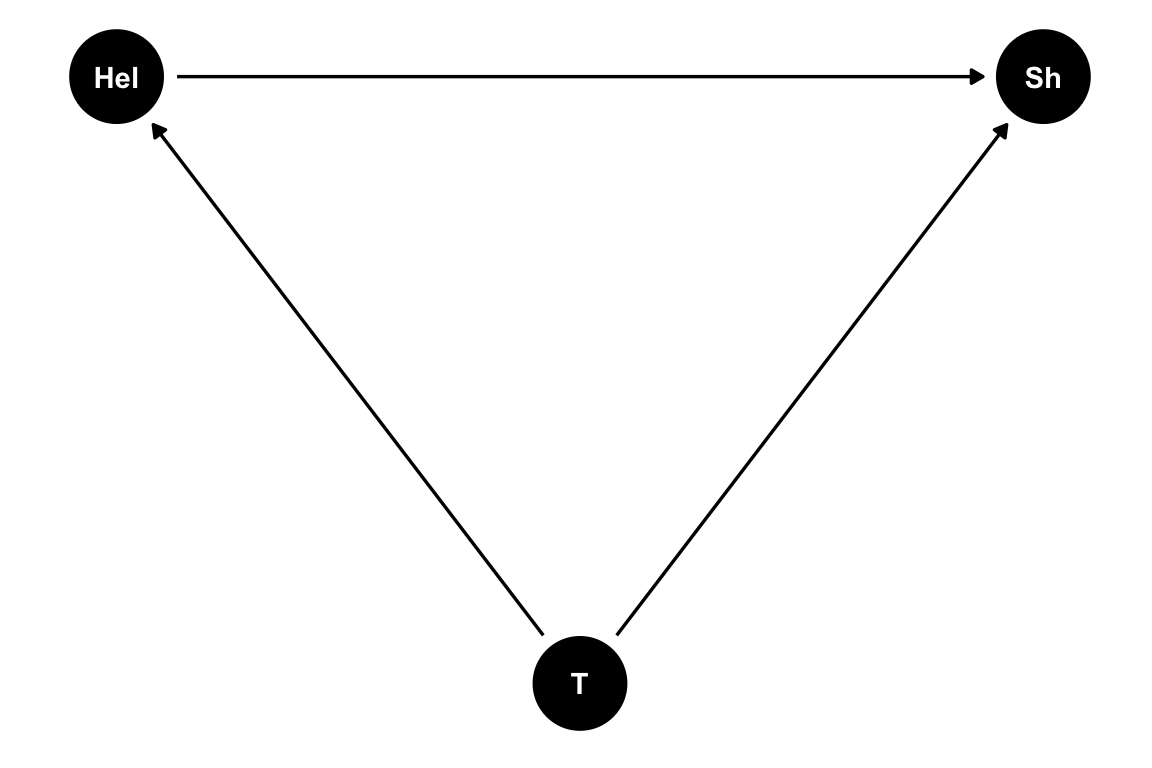
¿Así de simple? Sí y no ¿Qué pasa cuando las cosas se empiezan a complicar? Pensemos en el clásico ejemplo del mantra “correlación no implica causalidad” la relación entre venta de helados (Hel) y accidentes por mordidas de tiburón en Australia(Sh). Si nosotros planteáramos que el aumento de la venta de helados causa el aumento de los accidentes no tendría mucho sentido, ¿No?. Entonces, ¿Qué está pasando? ¿Qué pinta tiene el DAG? Bueno, como ya comentamos cuando hablamos de correlación en este caso lo que tenemos es una causa común a ambos fenómenos que, a modo de simplificar, la podríamos resumir como la temperatura (T). Entonces, cuando sube la temperatura sube la venta de helados, pero también los accidentes por mordidas de tiburón. Una posible relación causal entre ambas variables podría ser esta:
Todo muy lindo, pero ¿Para qué?
4.2 El criterio de las puertas de atrás
Una de las principales ventajas de plantear un DAg para estudiar una relación causal es que nos permite ajustar un modelo a partir del cual, lo que estamos estimando en uno de sus parámetros es un estimador de la relación causal que queremos estudiar. Empecemos planteando los caminos posibles para llegar desde Hel a Sh. En este caso serían dos:
\[ \begin{array} _Hel \longrightarrow Sh \\ Hel \longleftarrow T \longrightarrow Sh \end{array} \]
El primero es lo que se llama un camino directo y es lo relación causal que queremos estudiar. Por otro lado, el segundo (\(Hel \leftarrow T \rightarrow Sh\)) es lo que se llama una puerta de atrás y lo identíficamos porque, al menos en alguna de sus relaciones causales, la flechita va para la izquierda. Identificar estos caminos puerta de atrás es una parte fundamental de controlar la variabilidad espúrea en nuestras relaciones causales. En particular en este ejemplo, tenemos un claro confusor y lo que queremos es controlar por T.
Simulemos esta relación y veamos que pasa.
Ver el código
set.seed(1414)
helados <- tibble(
Temperatura = rnorm(1000, 20, 5),
Helados = 1 + 1*Temperatura + rnorm(1000),
Ataques = 1 + 2*Temperatura + 0*Helados + rnorm(1000)
)Veamos que Temperatura es una variable aleatoria con distribución normal con media \(20\) y desviación estándar \(5\). Tomamos \(1000\) muestras de la misma y después generamos las variables Helados y Ataques como una combinación lineal de Temperatura más un error aleatorio de media \(0\) y desviación estándar \(1\). En la definición de Ataques podemos ver explícitamente que la influencia de Helados en Ataques es \(0\). Sin embargo, miremos la relación que existe entre ambas variables:
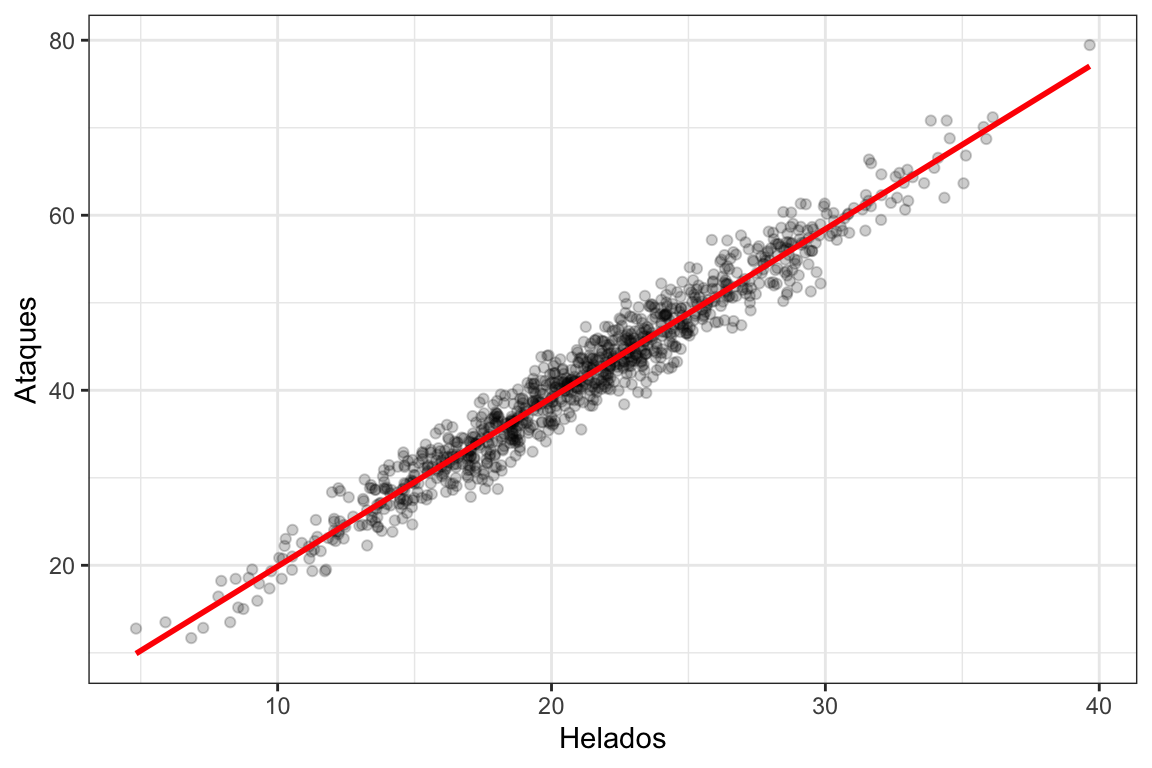
Vemos que ambas variables están altamente correlacionadas, de hecho, su r de Pearson vale 0.977. Sin embargo, nosotros sabemos que esa correlación es espúrea, que no hay una relación causal entre ventas de helados y ataques de tiburón y que algo tenemos que hacer. Hemos escuchado muchas veces que lo que tenemos que hacer es “controlar” por la temperatura, lo que en el contexto de la regresión lineal no significa otra cosa que agergar Temperatura como una covariable. Ajustemos dos modelos de regresión, uno con la Temperatura como covariable y uno sin y comparemos las estimaciones de los efectos causales (\(\hat\beta_H\))2 :
2 Recuerden que el diagrama causal no es un problema estadístico sino más bien se plantea previo a cualquier consideración estadística, usando como insumo el conocimiento del dominio que tenemos.
\[ \begin{array} _lm_1&:& Ataques_i = \alpha + \beta_{H} Helados_i + \epsilon_i \\ lm_2&:& Ataques_i = \alpha + \beta_{H} Helados_i + \beta_{T} Temperatura_i + \tau_i \end{array} \] En la siguiente tabla podemos ver las estimaciones de \(\hat\beta_H\) para cada uno de los modelos:
| Dependent variable: | ||
| Ataques | ||
| Sin controlar por Temp. | Controlando por Temp. | |
| (1) | (2) | |
| Helados | 1.928*** | -0.001 |
| (0.013) | (0.032) | |
| Temperatura | 2.003*** | |
| (0.033) | ||
| Constant | 0.602** | 1.015*** |
| (0.291) | (0.134) | |
| Observations | 1,000 | 1,000 |
| R2 | 0.954 | 0.990 |
| Adjusted R2 | 0.954 | 0.990 |
| Residual Std. Error | 2.246 (df = 998) | 1.032 (df = 997) |
| F Statistic | 20,826.210*** (df = 1; 998) | 51,243.220*** (df = 2; 997) |
| Note: | p<0.1; p<0.05; p<0.01 | |
Como podemos ver, si no controlamos por Temperatura , la estimación de \(\hat\beta_H\) tiene un valor cercano a \(1\), mientras que si controlamos por Temperatura tiene un valor cercano a \(0\) lo que sabemos es el valor “real” del parámetro \(\beta_H\). Todo muy lindo pero, ¿Qué tiene que ver esto con los DAGS? Bueno, cuando planteamos un DAG existe algo que se llama el criterio de las puertas traseras que dice que para estimar el efecto causal que nos interesa debemos “cerrar” todas las puertas traseras que conectan la causa y elefecto. Y “cerrar” en este contexto es simplemente controlar por la variabilidad de alguna de las variables presentes en la puerta trasera. En este caso, controlando por Temperatura estamos cerrando la única puerta trasera, por lo tanto, estamos estimando el verdadero efecto causal que nos interesa.
4.3 Colliders
Hasta ahora tuvimos que lidiar casi únicamente con confusores pero existe otro tipo de variables en el contexto de un camino causal que se denomina collider. Vemos un ejemplo y apliquemos el criterio de las puertas traseras. Pensemos el siguiente ejemplo. Supongamos que queremos estudiar el efecto del factor de riesgo edad (Age) en la infección de COVID-19 (Cov), pero lo hacemos a través de datos voluntarios recavados por una aplicación móvil (App). Un DAG muy simplicado que podríamos plantear es el siguiente:
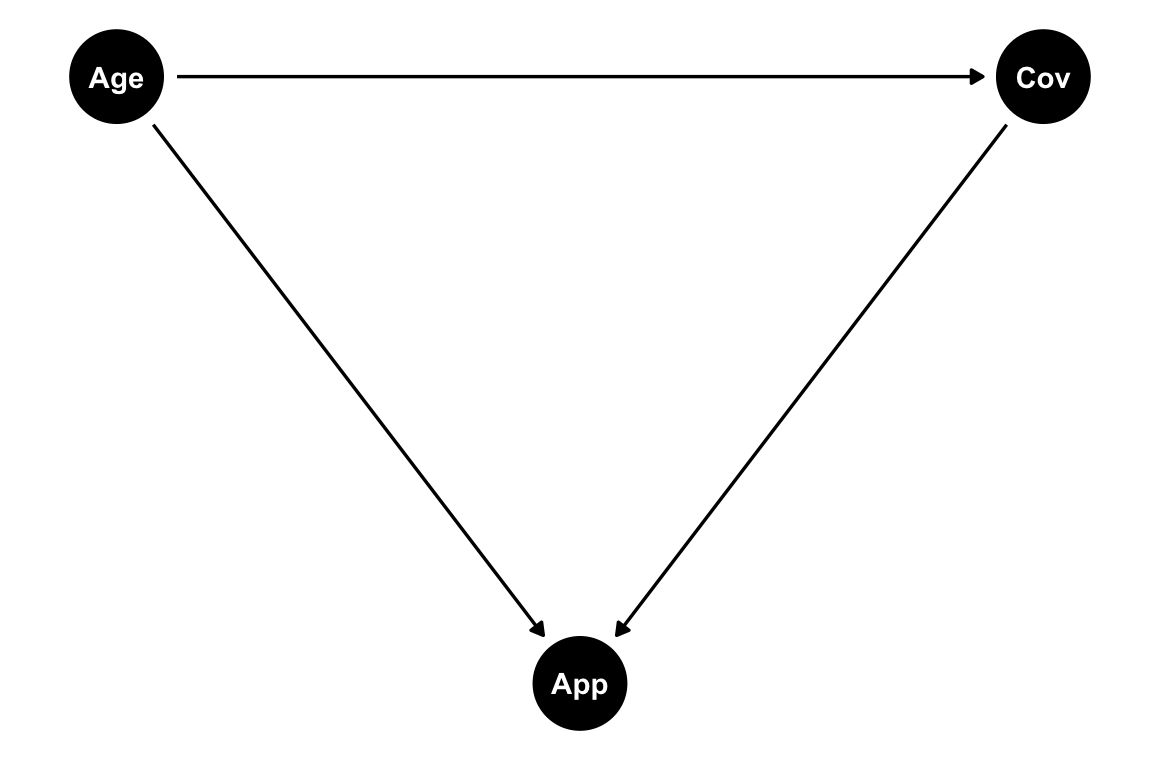
Ya que sabemos que la edad tienen un efecto en el uso de aplicaciones móviles y, podemos suponer, que la gente que se infecta de COVID-19 tiende a reportar más sus datos en la aplicación. Ahora veamos los caminos:
\[ \begin{array} _Age \longrightarrow Cov \\ Age \longrightarrow App \longleftarrow Cov \end{array} \] Repitamos el ejercicio de simulación que utilizamos en el ejemplo de los confusores, sólo que esta vez Covid es una variable dicotómica y, por lo tanto, debemos muestrarla de una distribución Bernoulli3:
3 Esto resulta especialmente útil cuando los DAGS se empiezan a complicar.
Ver el código
set.seed(123)
covid <- tibble(
Age = rnorm(1000, 40, 10),
Covid = rbinom(1000, 1, prob = 1/(1+exp(10-.25*Age))),
App = 1 - 1*Age + 1*Covid +rnorm(1000)
)Puede verse que la verdadera relación entre Covid y Age (en términos de parámetros de una regresión logística) es \(0.25\). Veamos como se ve la edad de los infectados y no infectados:
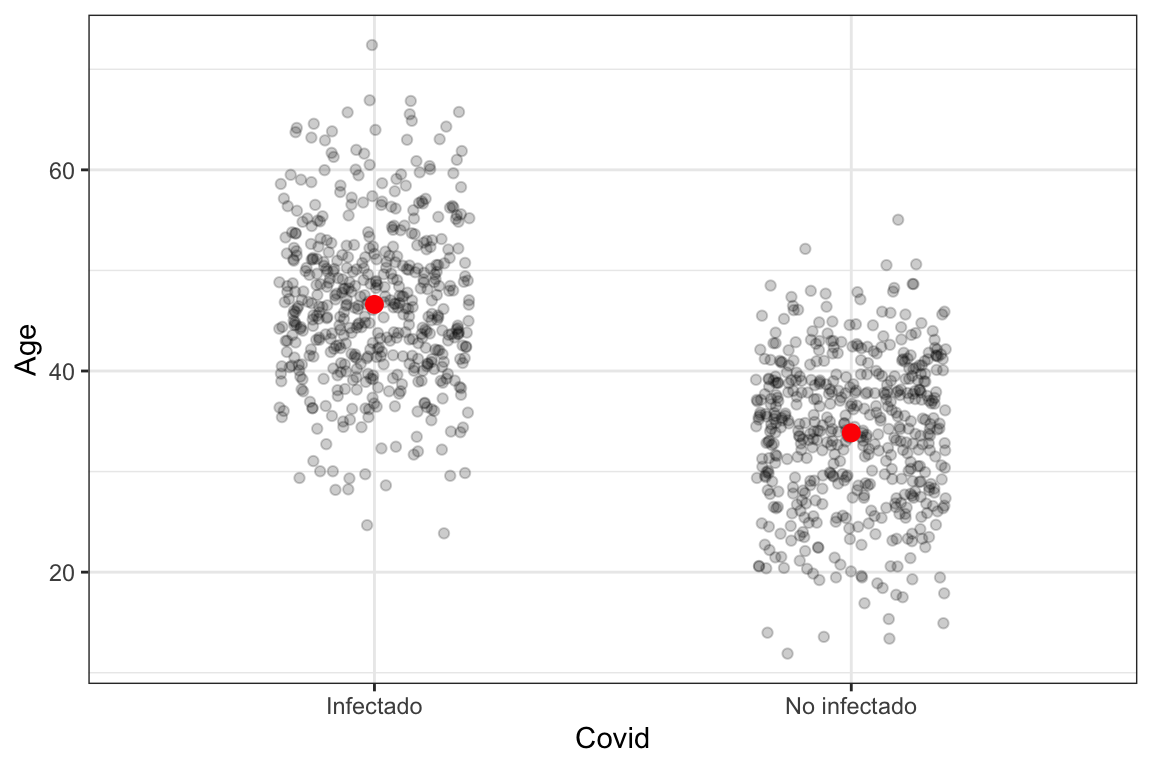
Según el criterio de las puertas traseras deberíamos controlar por App para así cerrar ese camino. Ajustemos estos dos regresiones logísticas y veamos sus estimaciones de los parámetros:
\[ \begin{array} _glm_1&:& logit(Covid_i) = \alpha + \beta_{Age} Age_i + \epsilon_i \\ glm_2&:& logit(Covid_i) = \alpha + \beta_{Age} Age_i + \beta_{App} App_i + \epsilon_i \end{array} \]
En la siguiente tabla podemos ver las estimaciones de \(\hat\beta_{Age}\) para cada uno de los modelos:
| Dependent variable: | ||
| Covid | ||
| Sin controlar por App | Controlando por App | |
| (1) | (2) | |
| Age | 0.243*** | 1.354*** |
| (0.016) | (0.109) | |
| App | 1.100*** | |
| (0.103) | ||
| Constant | -9.787*** | -11.839*** |
| (0.631) | (0.763) | |
| Observations | 1,000 | 1,000 |
| Log Likelihood | -419.336 | -344.156 |
| Akaike Inf. Crit. | 842.672 | 694.312 |
| Note: | p<0.1; p<0.05; p<0.01 | |
La estimación del efecto correcta sería la del modelos sin controlar pero ¿Por qué pasa esto? Cuando tenemos un collider podemos considerar ese camino como cerrado por defecto y al controlar por él, ese camino se abre. Entonces, en si bien teníamos dos posibles caminos causales, sólo uno estaba abierto y no necesitábamos controlar por App. Esto se debe a que, al App no causar ninguna de mis otras dos variables, ese camino causal está cerrado. Para reflexionar un poco en por qué ese camino se abre al controlar por un collider recomiendo las reflexiones del capítulo 8 de (Huntington-Klein 2021).
4.4 Un ejemplo
Analicemos un ejemplo que tiene un poquito de todo. En el mismo queremos estudiar la el efecto de las vitaminas (Vits) en los defectos de nacimiento (BD). Además de esta relación, podemos identificar otras variables que podrían influir en ellas: La dificultad para concebir un embarazo (DC); El cuidado pre-natal (PNC); el status socioeconómico (SES); y aspectos genéticos (Gen). El flujo de causalidad propuesto entre las variables puede verse representado en el siguiente DAG4:
4 Recuerden que el diagrama causal no es un problema estadístico sino más bien se plantea previo a cualquier consideración estadística, usando como insumo el conocimiento del dominio que tenemos.
Ver el código
dag_Vit <- dagitty::dagitty('dag {
BD [outcome,pos="0.109,0.631"]
DC [pos="0.117,-1.517"]
Gen [pos="0.850,-0.411"]
PNC [pos="-0.837,-0.433"]
SES [pos="-1.839,-1.468"]
Vits [exposure,pos="-1.844,0.645"]
DC -> PNC
Gen -> BD
Gen -> DC
PNC -> BD
PNC -> Vits
SES -> PNC
SES -> Vits
Vits -> BD
}')
tidy_dag <- tidy_dagitty(dag_Vit)
ggdag(tidy_dag) +
theme_dag()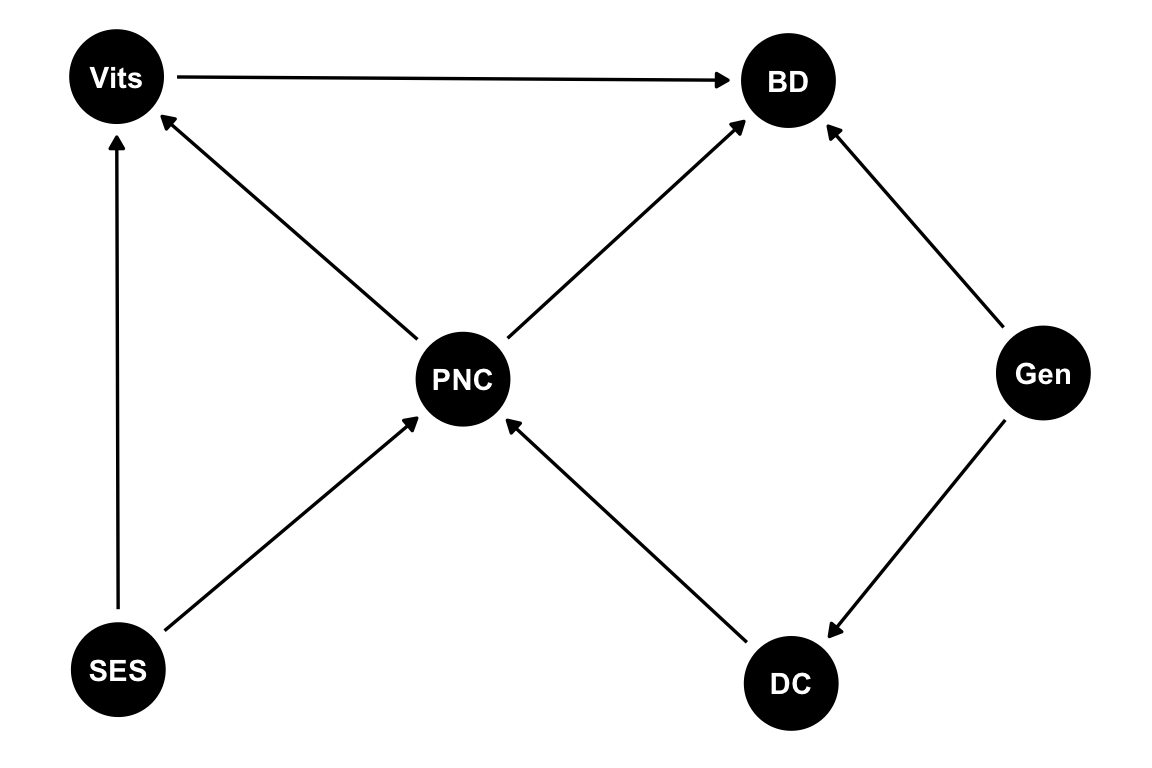
Si tenemos todos estos datos observados y queremos estimar el efecto causal de las vitaminas en los defectos de nacimiento, lo primero que tenemos que hacer es plantear todos los caminos abiertos. Esto lo podemos hacer a ojo, pero también nos podemos ayudar con la función ggdag_paths del paquete {ggdags}5. A continuación vemos un ejemplo de uso de esta función:
5 Esto resulta especialmente útil cuando los DAGS se empiezan a complicar.
Ver el código
dag_Vit %>% ggdag_paths(from = "Vits", to = "BD", shadow = TRUE) +
theme_dag() +
theme(legend.position = "bottom")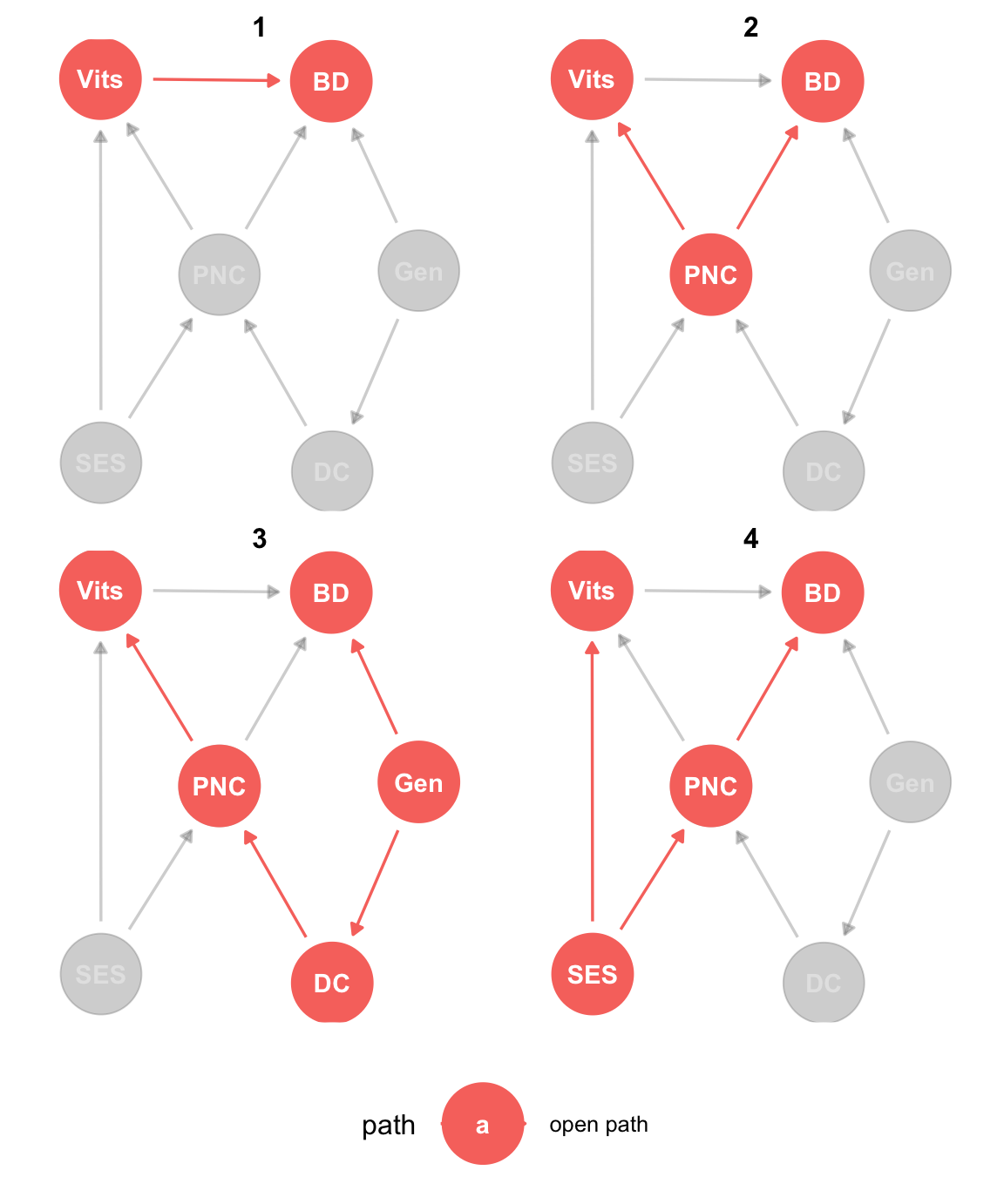
Podemos ver que los caminos abiertos son:
\[ \begin{array} _Vits \longrightarrow BD\\ Vits \longleftarrow PNC \longrightarrow BD\\ Vits \longleftarrow PNC \longleftarrow DC \longleftarrow Gen \longrightarrow BD \\ Vits \longleftarrow SES \longrightarrow PNC \longrightarrow BD \end{array} \]
Pero ¿Por qué no está abierto el camino \(Vits \leftarrow SES \rightarrow PNC \leftarrow DC \leftarrow Gen \rightarrow BD\)? ¡Exacto! Está cerrado, porque para ese camino PNC es un collider, ya que está causada tanto por SES como por DC. Resulta importante notar que una variable es un collider o no en el contexto de un camino de causalidad y no lo es siempre. De hecho, podemos ver que PNC actúa como un confusor en el camino \(Vits \leftarrow PNC \rightarrow BD\). La función ggdag_collider también nos puede ayudar a identificar un collider.
Ver el código
dag_Vit %>% ggdag_collider() +
theme_dag() +
scale_color_brewer(palette = "Dark2")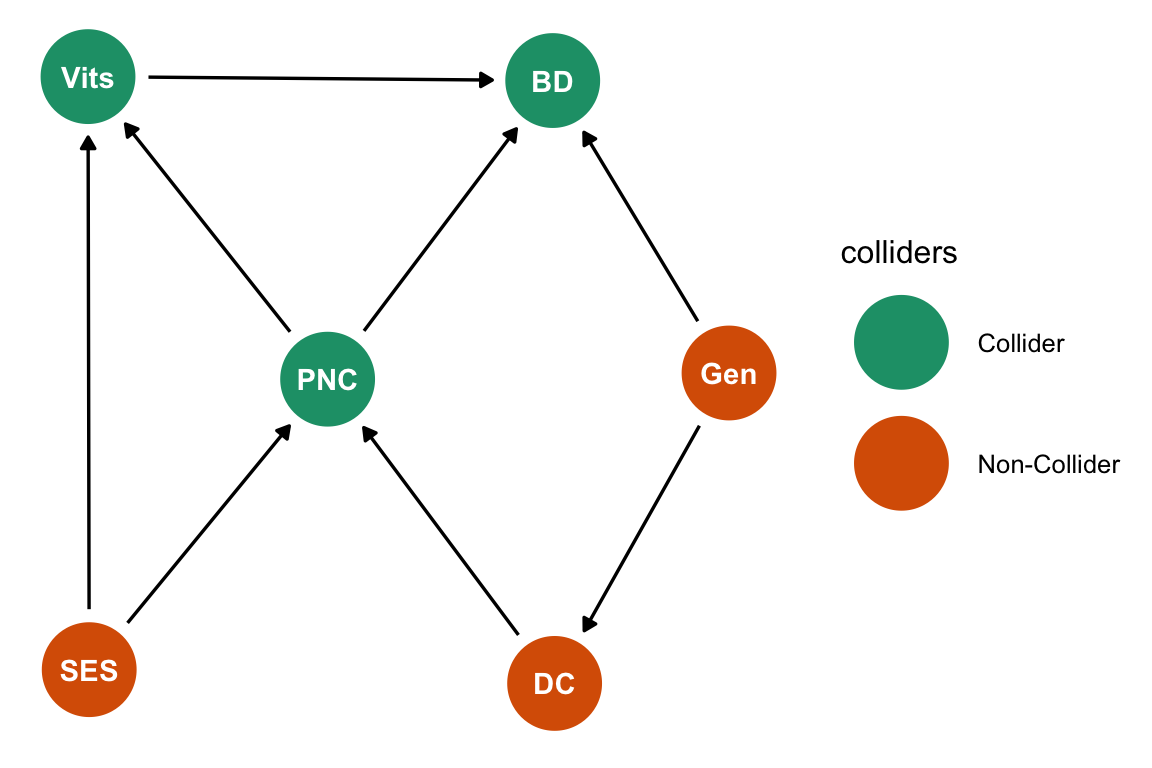
Entonces tenemos cuatro caminos abiertos, el que queremos estudiar y tres puertas de atrás. Sin embargo, todo indica que tenemos que controlar por PNC y listo ¿No? Apliquemos esto agregando el parámetro adjust_for = "PNC" a la función ggdag_paths:
Ver el código
dag_Vit %>% ggdag_paths(from = "Vits", to = "BD",
adjust_for = "PNC", shadow = TRUE) +
theme_dag() +
labs(hue = NULL) +
theme(legend.position = "bottom")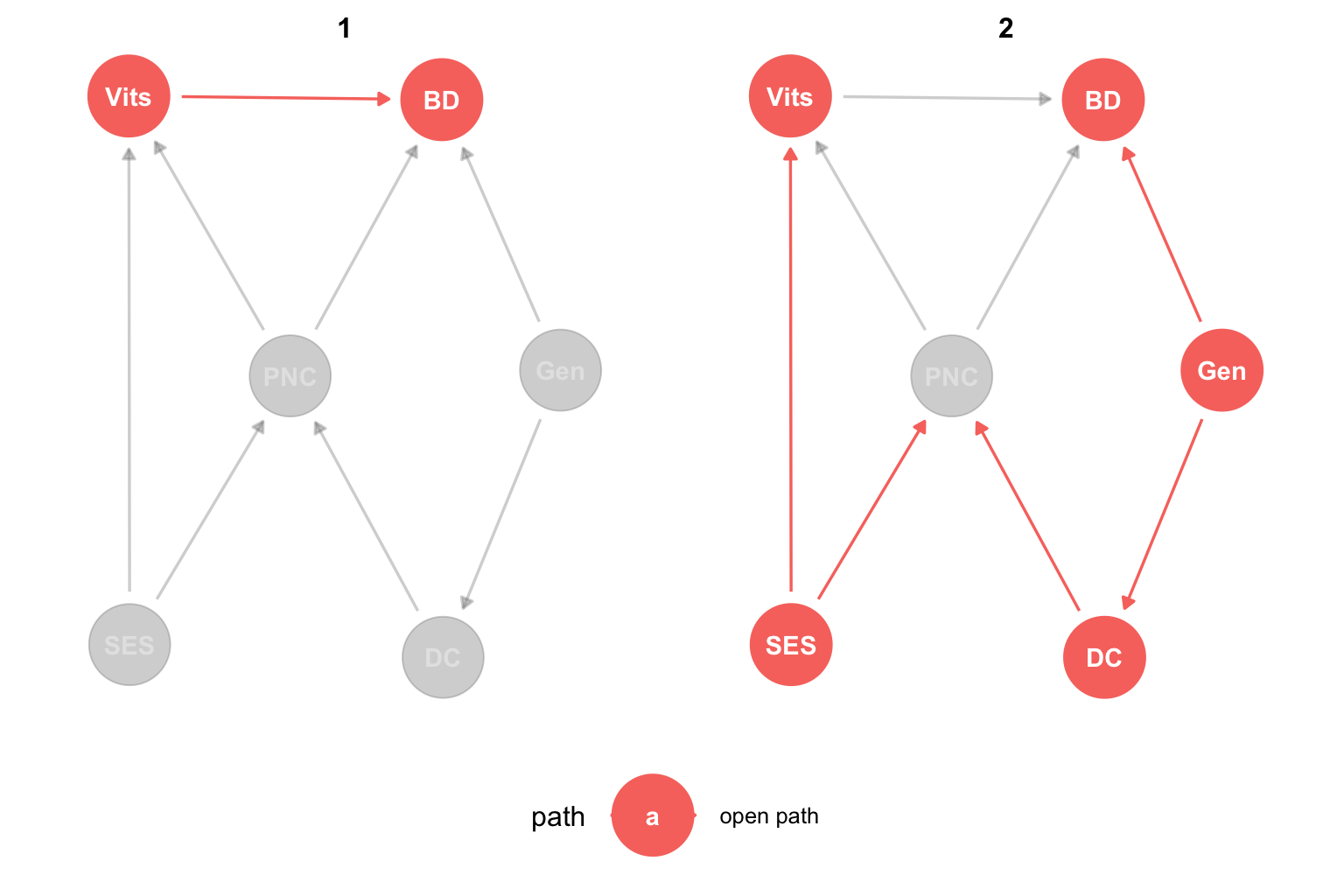
Sin embargo, podemos ver que, aún controlando por PNC, los caminos abiertos son:
\[ \begin{array} _Vits \longrightarrow BD\\ Vits \leftarrow SES \rightarrow PNC \leftarrow DC \leftarrow Gen \rightarrow BD \end{array} \]
¿Qué pasó? Bueno, lo que pasó es que al controlar por un collider abrimos un camino que estaba cerrado. Miremos qué pasa si controlamos por PNC y DC:
Ver el código
dag_Vit %>% ggdag_paths(from = "Vits", to = "BD",
adjust_for = c("PNC", "DC"), shadow = TRUE) +
theme_dag() +
labs(hue = NULL) +
theme(legend.position = "bottom")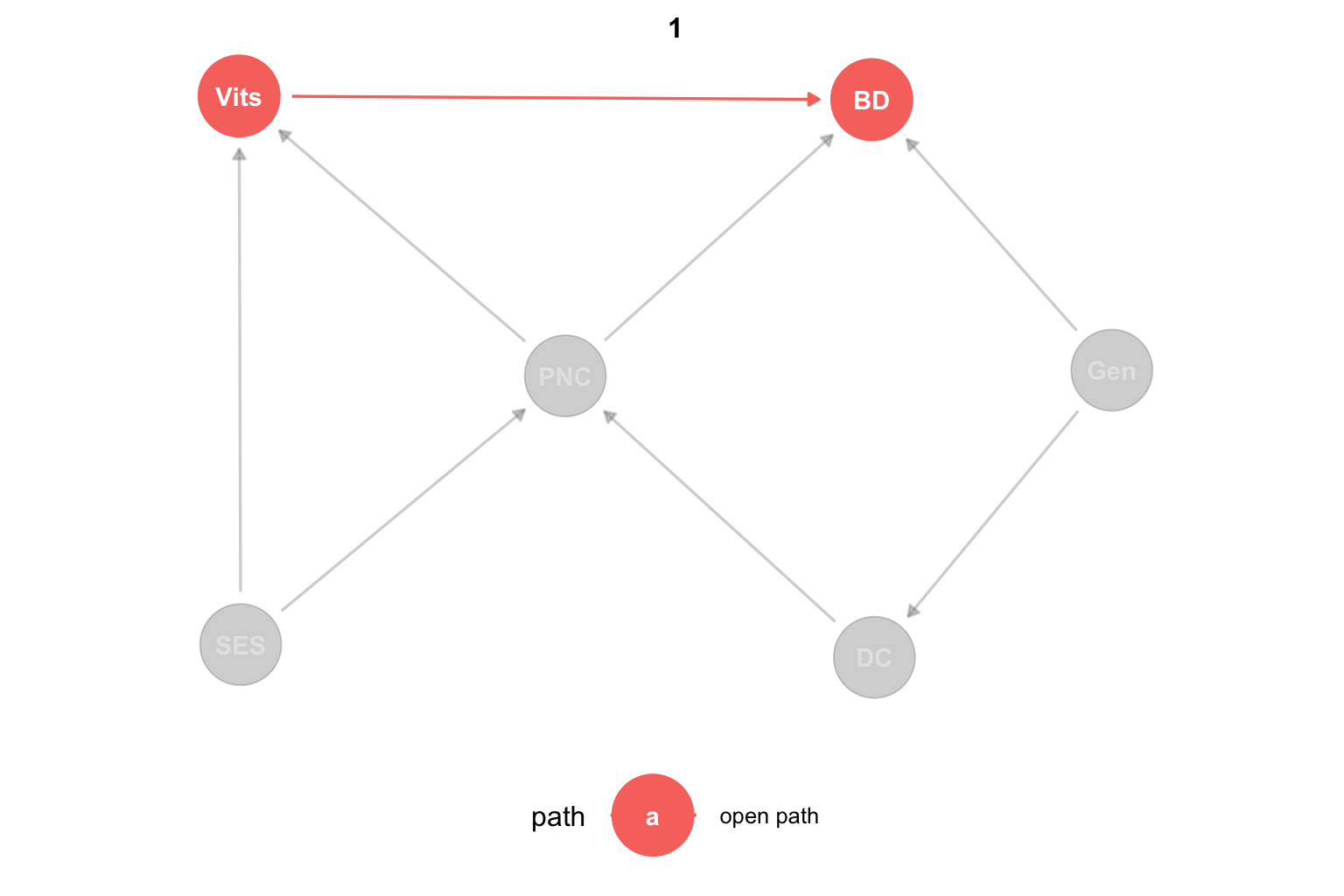
Ahora sí, el único camino abierto es \(Vits \rightarrow BD\), que es la relación causal que queremos estudiar. Finalmente, el modelo que deberíamos ajustar es:
\[ BD_i = \alpha + \beta_{Vits} Vits_i + \beta_{PNC} PNC_i + \beta_{DC} DC_i + \epsilon_i \]
Donde \(\beta_{Vits}\) es un estimador del efecto causal que queremos estudiar.
Para más ejemplos y detalles sobre los DAGS pueden consultar (Cunningham 2021) o (Huntington-Klein 2021). El canal de YouTube de Nick Huntington-Klein también es un excelente recurso para profundizar sobre estos temas6.
6 Nick es el autor de (Huntington-Klein 2021).